Amount of Substance - The Ideal Gas Equation (A-Level Chemistry)

The Ideal Gas  Equation

Ideal Gas Equation

Ideal Gases

An ideal gas is a hypothetical gas whose volume varies in proportion to its  temperature and in inverse proportion to its pressure. For a gas to be an ideal gas, as opposed to a real gas, its particles must follow certain rules:

  • Lack of intermolecular forces. Gas molecules must neither repel or attract each other.
  • Elastic collisions. The only interaction between gas molecules are elastic collisions. No energy is lost when particles collide against each other or against the surface of the container so that kinetic energy remains constant.
  • Zero particle volume. Individual gas particles are so small in comparison to the empty space between them, that their volume is negligible.

No gas can behave exactly like an ideal gas but the lower their intermolecular forces, the more they can approach ideal behavior. Nobel gases for examples, have very low intermolecular forces and hence approach ideal behavior.

At room temperatures and pressures, many of the gases we care about can be assumed to behave ideally.

Understanding the Ideal Gas Equation

The ideal gas equation is used to calculate the number of moles found in a specific volume of a gas:

 

Amount of Substance - The Ideal Gas Equation
Amount of Substance – The Ideal Gas Equation

You need to know what each letter in the equation represents as well as the units used:

p = pressure (Pa)

V = volume (m3)

n = number of moles

R = 8.31 J K-1mol-1 (this is the gas constant that will be given to you in the exam)

T = temperature (K)

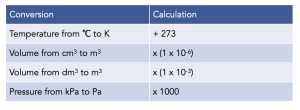
Unit Conversions for the Ideal Gas Equation

A-level Chemistry - The Ideal Gas Equation
Amount of Substance – The Ideal Gas Equation

Step by Step Example

Practice Question: A gas occupies a volume of 1250cm3 at a temperature of 45℃ and a pressure of 105kPa. The gas has a mass of 2.4g. The gas constant (R) = 8.31 J K-1mol-1 . What is the relative molecular mass of the gas?

1. First write down all the values that you are given as written in the question.

Volume in cm3 = 1250cm3

Temperature in ℃ = 45℃

Pressure in kPa = 105kPa

Mass in g = 2.4g

R = 8.31 J K-1mol-1

2. Next convert all the values so that they are in the same units as  the units used in the ideal gas equation.

Volume in m3 (V) = 1250 x (1 x 10-6) = 1.25 x 10-3

Temperature in K (T) = 45 + 273 = 318

Pressure in Pa (p) = 105 x 1000 = 105000 Pa

Mass in g = 2.4g

R = 8.31 J K-1mol-1

3. Then rearrange the ideal gas equation based on the values that are known.

pV = nRT

n = pV/RT

4. Finally enter the values into the equation

n = (105000 x (1.25 x 10-3)) ÷ (8.31 x 318) = 0.0497 moles (to 3 significant figures)

5. To calculate relative molecular mass use the equation: Relative molecular mass of gas = mass ÷ number of moles

Relative molecular mass of gas = mass ÷ number of moles = 2.4 ÷ 0.0497 = 48.3

Still got a question? Leave a comment

Leave a comment

Post as “Anonymous”

AQA 3.1.1 Atomic structure

Ionisation Energies (A-Level Chemistry)

Atomic Structure – Electron Arrangement (A-Level Chemistry)

Atomic Structure – Electrons in Atoms (A-Level Chemistry)

Atomic Structure – Mass Spectrometry (A-Level Chemistry)

Atomic Structure – Element Isotopes (A-Level Chemistry)

Atomic Structure – Atomic and Mass Number (A-Level Chemistry)

Atomic Structure – Subatomic Particles (A-Level Chemistry)

AQA 3.1.10 Equilibrium constant Kp for homogeneous systems

Equilibrium Constant for Homogenous Systems – Le Chatelier’s Principle in Gas Equilibria (A-Level Chemistry)

Equilibrium Constant for Homogenous Systems – Gas Equilibria and Kp (A-Level Chemistry)

Equilibrium Constant for Homogeneous System – Changing Kp (A-Level Chemistry)

Equilibrium Constant for Homogenous Systems – Gas Partial Pressures (A-Level Chemistry)

AQA 3.1.11 Electrode potentials and electrochemical cells

Acids and Bases – Drawing pH Curves (A-Level Chemistry)

Acids and Bases – Acid-Base Indicators (A-Level Chemistry)

Acids and Bases – Dilutions and pH (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Commercial Applications of Fuel Cells (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Electrochemical Cells Reactions (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Representing Electrochemical Cells (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Electrode Potentials (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Half Cells and Full Cells (A-Level Chemistry)

AQA 3.1.12 Acids and bases

Acids and Bases – Titrations (A-Level Chemistry)

Acids and Bases – Buffer Action (A-Level Chemistry)

Acids and Bases – pH of Strong Bases (A-Level Chemistry)

Acids and Bases – Ionic Product of Water (A-Level Chemistry)

Acids and Bases – More Ka Calculations (A-Level Chemistry)

Acids and Bases – The Acid Dissociation Constant, Ka (A-Level Chemistry)

Acids and Bases – The pH Scale and Strong Acids (A-Level Chemistry)

Acids and Bases – Neutralisation Reactions (A-Level Chemistry)

Acids and Bases – Acid and Base Strength (A-Level Chemistry)

Acids and Bases – The Brønsted-Lowry Acid-Base Theory (A-Level Chemistry)

AQA 3.1.2 Amount of substance

Amount of Substance – Percentage Atom Economy (A-Level Chemistry)

Amount of Substance – Calculating Percentage Yields (A-Level Chemistry)

Amount of Substance – Stoichiometric Calculations (A-Level Chemistry)

Amount of Substance – Balancing Chemical Equations (A-Level Chemistry)

Amount of Substance – Empirical and Molecular Formulae (A-Level Chemistry)

Amount of Substance – Further Mole Calculations (A-Level Chemistry)

Amount of Substance- The Mole and The Avogadro Constant (A-Level Chemistry)

Amount of Substance – Measuring Relative Masses (A-Level Chemistry)

Amount of Substance – The Ideal Gas Equation (A-Level Chemistry)

AQA 3.1.3 Bonding

Periodicity – Classification (A-Level Chemistry)

Bonding – Hydrogen Bonding in Water (A-Level Chemistry)

Bonding – Forces Between Molecules (A-Level Chemistry)

Bonding – Bond Polarity (A-Level Chemistry)

Bonding – Molecular Shapes (A-Level Chemistry)

Bonding – Predicting Structures (A-Level Chemistry)

Bonding – Carbon Allotropes (A-Level Chemistry)

Bonding – Properties of Metallic Bonding (A-Level Chemistry)

Bonding – Properties of Covalent Structures (A-Level Chemistry)

Bonding – Covalent Bonds (A-Level Chemistry)

AQA 3.1.4 Energetics

AQA 3.1.5 Kinetics

Kinetics – The Maxwell–Boltzmann Distribution and Catalysts (A-Level Chemistry)

Kinetics – The Collision Theory and Reaction Rates (A-Level Chemistry)

AQA 3.1.6 Chemical equilibria

Calculations with Equilibrium Constants (A-Level Chemistry)

Chemical Equilibria applied to Industry (A-Level Chemistry)

Chemical Equilibria and Le Chatelier’s Principle (A-Level Chemistry)

AQA 3.1.7 Oxidation, reduction and redox

Oxidation, Reduction and Redox Equations – Balancing Redox Equations (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Redox Processes (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Oxidation States (A-Level Chemistry)

AQA 3.1.8 Thermodynamics

Thermodynamic – Calculations involving Free Energy (A-Level Chemistry)

Thermodynamic – Gibbs Free Energy (A-Level Chemistry)

Thermodynamic – Entropy Change Predictions (A-Level Chemistry)

Thermodynamic – Total Entropy Changes (A-Level Chemistry)

Thermodynamic – Introduction to Entropy (A-Level Chemistry)

Thermodynamic – Calculating Enthalpy Changes of Solution (A-Level Chemistry)

Thermodynamic – Enthalpy of Solution (A-Level Chemistry)

Thermodynamic – Enthalpy of Hydration (A-Level Chemistry)

Thermodynamic – Calculations involving Born-Haber Cycles (A-Level Chemistry)

Thermodynamic – Construction of Born-Haber Cycles (A-Level Chemistry)

AQA 3.1.9 Rate equations

Rate Equations – Reaction Determining Steps (A-Level Chemistry)

Rate Equations – Reaction Half Lives (A-Level Chemistry)

Rate Equations – Uses of Clock Reactions (A-Level Chemistry)

Rate Equations – Determining Orders of Reactions Graphically (A-Level Chemistry)

Rate Equations – Determining Order of Reaction Experimentally (A-Level Chemistry)

Rate Equations – Temperature Changes and the Rate Constant (A-Level Chemistry)

Rate Equations – The Rate Constant (A-Level Chemistry)

Rate Equations – Introduction to Orders of Reactions (A-Level Chemistry)

Rate Equations – The Rate Equation (A-Level Chemistry)

Rate Equations – Measuring Rate of Reaction (A-Level Chemistry)

AQA 3.2.1 Periodicity

Periodicity – Trends Along Period 3 (A-Level Chemistry)

Periodicity – Classification (A-Level Chemistry)

AQA 3.2.2 Group 2, the alkaline earth metals

Uses of Group 2 Elements and their Compounds (A-Level Chemistry)

Reactions of Group 2 Elements (A-Level Chemistry)

Group 2, The Alkaline Earth Metals (A-Level Chemistry)

Ionisation Energies (A-Level Chemistry)

AQA 3.2.3 Group 7(17), the halogens

The Halogens -Halide Ions and their Reactions (A-Level Chemistry)

The Halogens – Disproportionation Reactions in Halogens (A-Level Chemistry)

The Halogens – Reactions with Halogens (A-Level Chemistry)

The Halogens – Group 7, The Halogens (A-Level Chemistry)

AQA 3.2.4 Properties of Period 3 elements

Properties of Period 3 Elements – Properties of Period 3 Compounds (A-Level Chemistry)

Properties of Period 3 Elements – Reactivity of Period 3 Elements (A-Level Chemistry)

AQA 3.2.5 Transition metals

Transition Metals – Autocatalysis of Transition Metals (A-Level Chemistry)

Transition Metals – Transition Metals as Homogeneous Catalysts (A-Level Chemistry)

Transition Metals – Transition Metals as Heterogeneous Catalysts (A-Level Chemistry)

Transition Metals – Examples of Redox Reactions in Transition Metals (A-Level Chemistry)

Transition Metals – Iodine-Sodium Thiosulfate Titrations (A-Level Chemistry)

Transition Metals – Carrying Titrations with Potassium Permanganate (A-Level Chemistry)

Transition Metals – Redox Titrations (A-Level Chemistry)

Transition Metals – Redox Potentials (A-Level Chemistry)

Transition Metals – Redox Reactions Revisited (A-Level Chemistry)

Transition Metals – Ligand Substitution Reactions (A-Level Chemistry)

AQA 3.2.6 Reactions of ions in aqueous solution

Reactions of Ions in Aqueous Solutions – Metal Ions in Solution (A-Level Chemistry)

AQA 3.3.1 Introduction to organic chemistry

Introduction to Organic Chemistry – Structural Isomers (A-Level Chemistry)

Introduction to Organic Chemistry – E/Z Isomerism (A-Level Chemistry)

Introduction to Organic Chemistry – Reaction Mechanisms in Organic Chemistry (A-Level Chemistry)

Introduction to Organic Chemistry – General Formulae (A-Level Chemistry)

Introduction to Organic Chemistry – Introduction to Functional Groups (A-Level Chemistry)

Introduction to Organic Chemistry – Naming and Representing Organic Compounds (A-Level Chemistry)

AQA 3.3.10 Aromatic chemistry

Aromatic Chemistry – Friedel-Crafts Acylation and Alkylation (A-Level Chemistry)

Aromatic Chemistry – Halogenation Reactions in Benzene (A-Level Chemistry)

Aromatic Chemistry – Electrophilic Substitution Reactions in Benzene (A-Level Chemistry)

Aromatic Chemistry – Improved Benzene Model (A-Level Chemistry)

Aromatic Chemistry – Introduction to Benzene (A-Level Chemistry)

AQA 3.3.11 Amines

Amines – Nitriles (A-Level Chemistry)

Amines – Properties and Reactivity of Amines (A-Level Chemistry)

Amines – Amine Synthesis (A-Level Chemistry)

Amines – Introduction to Amines (A-Level Chemistry)

AQA 3.3.12 Polymers

Polymer Disposal (A-Level Chemistry)

Polymer Biodegradability (A-Level Chemistry)

Condensation Polymers (A-Level Chemistry)

Polyamide Formation (A-Level Chemistry)

AQA 3.3.13 Amino acids

Amino Acids, Proteins and DNA – DNA Replication (A-Level Chemistry)

Amino Acids, Proteins and DNA – DNA (A-Level Chemistry)

Amino Acids, Proteins and DNA – Enzyme Action (A-Level Chemistry)

Amino Acids, Proteins and DNA – Structure of Proteins (A-Level Chemistry)

Amino Acids, Proteins and DNA – Structure of Amino Acids (A-Level Chemistry)

AQA 3.3.14 Organic synthesis

Organic Synthesis – Considerations in Organic Synthesis (A-Level Chemistry)

Organic Synthesis – Organic Synthesis: Aromatic Compounds (A-Level Chemistry)

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

AQA 3.3.15 NMR

Analytical Techniques – High Resolution ¹H NMR (A-Level Chemistry)

Analytical Techniques – Types of NMR: Hydrogen (A-Level Chemistry)

Analytical Techniques – Types of NMR: Carbon 13 (A-Level Chemistry)

Analytical Techniques – NMR Samples and Standards (A-Level Chemistry)

Analytical Techniques – Nuclear Magnetic Resonance Spectroscopy (A-Level Chemistry)

AQA 3.3.16 Chromatography

Analytical Techniques – Different Types of Chromatography (A-Level Chemistry)

Analytical Techniques – Chromatography (A-Level Chemistry)

AQA 3.3.2 Alkanes

Alkanes – Obtaining Alkanes (A-Level Chemistry)

Alkanes – Alkanes: Properties and Reactivity (A-Level Chemistry)

AQA 3.3.3 Halogenoalkanes

Halogenoalkanes – Environmental Impact of Halogenalkanes (A-Level Chemistry)

Halogenoalkanes – Reactivity of Halogenoalkanes (A-Level Chemistry)

Halogenoalkanes – Introduction to Halogenoalkanes (A-Level Chemistry)

AQA 3.3.4 Alkenes

Alkenes – Addition Polymerisation in Alkenes (A-Level Chemistry)

Alkenes – Alkene Structure and Reactivity (A-Level Chemistry)

Introduction to Organic Chemistry – E/Z Isomerism (A-Level Chemistry)

AQA 3.3.5 Alcohols

Alcohols – Industrial Production of Alcohols (A-Level Chemistry)

Alcohols – Alcohol Reactivity (A-Level Chemistry)

Alcohols – Alcohol oxidation (A-Level Chemistry)

Alcohols – Introduction to Alcohols (A-Level Chemistry)

AQA 3.3.6 Organic analysis

Organic Analysis – Infrared (IR) Spectroscopy (A-Level Chemistry)

Organic Analysis – Identification of Functional Groups (A-Level Chemistry)

AQA 3.3.7 Optical isomerism

Optical Isomerism (A-Level Chemistry)

AQA 3.3.8 Aldehydes and ketones

Aldehydes and Ketones – Reactions to Increase Carbon Chain Length (A-Level Chemistry)

Aldehydes and Ketones – Testing for Carbonyl Compounds (A-Level Chemistry)

Aldehydes and Ketones – Reactivity of Carbonyl Compunds (A-Level Chemistry)

Aldehydes and Ketones – Carbonyl Compounds (A-Level Chemistry)

AQA 3.3.9 Carboxylic acids

Carboxylic Acids and Derivatives – Structure of Amides (A-Level Chemistry)

Carboxylic Acids and Derivatives – Acyl Groups (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Esters (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Carboxylic Acids (A-Level Chemistry)

21: Organic Synthesis

Organic Synthesis – Organic Synthesis: Aromatic Compounds (A-Level Chemistry)

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Organic Analysis – Identification of Functional Groups (A-Level Chemistry)

29: Intro to Organic Chemistry

Aromatic Chemistry – Electrophilic Substitution Reactions in Benzene (A-Level Chemistry)

Aromatic Chemistry – Benzene Nomenclature (A-Level Chemistry)

Aromatic Chemistry – Improved Benzene Model (A-Level Chemistry)

Optical Isomerism (A-Level Chemistry)

Introduction to Organic Chemistry – Naming and Representing Organic Compounds (A-Level Chemistry)

CIE 1: Atomic Structure

Ionisation Energies (A-Level Chemistry)

Periodicity – Classification (A-Level Chemistry)

Bonding – Ion Formation (A-Level Chemistry)

Atomic Structure – Electron Arrangement (A-Level Chemistry)

Atomic Structure – Electrons in Atoms (A-Level Chemistry)

Atomic Structure – Element Isotopes (A-Level Chemistry)

Atomic Structure – Atomic and Mass Number (A-Level Chemistry)

Atomic Structure – Subatomic Particles (A-Level Chemistry)

CIE 10: Group 2

Reactions of Group 2 Elements (A-Level Chemistry)

Group 2, The Alkaline Earth Metals (A-Level Chemistry)

CIE 11: Group 17

The Halogens -Halide Ions and their Reactions (A-Level Chemistry)

The Halogens – Disproportionation Reactions in Halogens (A-Level Chemistry)

The Halogens – Reactions with Halogens (A-Level Chemistry)

The Halogens – Group 7, The Halogens (A-Level Chemistry)

CIE 12

CIE 13: Intro to AS Organic Chemistry

Optical Isomerism (A-Level Chemistry)

Alkanes – Alkanes: Properties and Reactivity (A-Level Chemistry)

Introduction to Organic Chemistry – Structural Isomers (A-Level Chemistry)

Introduction to Organic Chemistry – E/Z Isomerism (A-Level Chemistry)

Introduction to Organic Chemistry – Reaction Mechanisms in Organic Chemistry (A-Level Chemistry)

Introduction to Organic Chemistry – General Formulae (A-Level Chemistry)

Introduction to Organic Chemistry – Introduction to Functional Groups (A-Level Chemistry)

Introduction to Organic Chemistry – Naming and Representing Organic Compounds (A-Level Chemistry)

Bonding – Covalent Bonds (A-Level Chemistry)

CIE 14: Hydrocarbons

Alkenes – Addition Polymerisation in Alkenes (A-Level Chemistry)

Alkenes – Alkene Structure and Reactivity (A-Level Chemistry)

Alkanes – Obtaining Alkanes (A-Level Chemistry)

Alkanes – Alkanes: Properties and Reactivity (A-Level Chemistry)

CIE 15: Halogen compounds

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Halogenoalkanes – Reactivity of Halogenoalkanes (A-Level Chemistry)

Halogenoalkanes – Introduction to Halogenoalkanes (A-Level Chemistry)

CIE 16: Hydroxy compounds

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Aldehydes and Ketones – Testing for Carbonyl Compounds (A-Level Chemistry)

Alcohols – Alcohol Reactivity (A-Level Chemistry)

Alcohols – Alcohol oxidation (A-Level Chemistry)

Alcohols – Introduction to Alcohols (A-Level Chemistry)

CIE 17: Carbonyl compounds

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Aldehydes and Ketones – Testing for Carbonyl Compounds (A-Level Chemistry)

Aldehydes and Ketones – Reactivity of Carbonyl Compunds (A-Level Chemistry)

CIE 18: Carboxylic acids and derivatives

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Carboxylic Acids (A-Level Chemistry)

CIE 19: Nitrogen Compounds

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Amines – Nitriles (A-Level Chemistry)

Amines – Amine Synthesis (A-Level Chemistry)

CIE 2: Atoms, molecules and stoichiometry

Bonding – Ion Formation (A-Level Chemistry)

Amount of Substance – Calculating Percentage Yields (A-Level Chemistry)

Amount of Substance – Stoichiometric Calculations (A-Level Chemistry)

Amount of Substance – Balancing Chemical Equations (A-Level Chemistry)

Amount of Substance – Empirical and Molecular Formulae (A-Level Chemistry)

Amount of Substance – Further Mole Calculations (A-Level Chemistry)

Amount of Substance- The Mole and The Avogadro Constant (A-Level Chemistry)

Amount of Substance – Measuring Relative Masses (A-Level Chemistry)

CIE 20: Polymerisation

Polymer Disposal (A-Level Chemistry)

Polymer Biodegradability (A-Level Chemistry)

Condensation Polymers (A-Level Chemistry)

CIE 22: Analytical Techniques

Organic Analysis – Infrared (IR) Spectroscopy (A-Level Chemistry)

Atomic Structure – Mass Spectrometry (A-Level Chemistry)

CIE 23: Chemical Energetics

Thermodynamic – Calculations involving Free Energy (A-Level Chemistry)

Thermodynamic – Gibbs Free Energy (A-Level Chemistry)

Thermodynamic – Entropy Change Predictions (A-Level Chemistry)

Thermodynamic – Total Entropy Changes (A-Level Chemistry)

Thermodynamic – Introduction to Entropy (A-Level Chemistry)

Thermodynamic – Calculating Enthalpy Changes of Solution (A-Level Chemistry)

Thermodynamic – Enthalpy of Solution (A-Level Chemistry)

Thermodynamic – Enthalpy of Hydration (A-Level Chemistry)

Thermodynamic – Calculations involving Born-Haber Cycles (A-Level Chemistry)

Thermodynamic – Construction of Born-Haber Cycles (A-Level Chemistry)

CIE 24: Electrochemistry

Electrode Potentials and Electrochemical Cells – Electrochemical Cells Reactions (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Representing Electrochemical Cells (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Electrode Potentials (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Half Cells and Full Cells (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Balancing Redox Equations (A-Level Chemistry)

CIE 25: Equilibria

Acids and Bases – Titrations (A-Level Chemistry)

Acids and Bases – Buffer Action (A-Level Chemistry)

Acids and Bases – Dilutions and pH (A-Level Chemistry)

Acids and Bases – pH of Strong Bases (A-Level Chemistry)

Acids and Bases – The Acid Dissociation Constant, Ka (A-Level Chemistry)

Acids and Bases – The pH Scale and Strong Acids (A-Level Chemistry)

Acids and Bases – Acid and Base Strength (A-Level Chemistry)

Acids and Bases – The Brønsted-Lowry Acid-Base Theory (A-Level Chemistry)

CIE 27: Group 2 Elements

Reactions of Group 2 Elements (A-Level Chemistry)

Group 2, The Alkaline Earth Metals (A-Level Chemistry)

CIE 28: Chemistry of transition elements

Transition Metals – Examples of Redox Reactions in Transition Metals (A-Level Chemistry)

Transition Metals – Iodine-Sodium Thiosulfate Titrations (A-Level Chemistry)

Transition Metals – Carrying Titrations with Potassium Permanganate (A-Level Chemistry)

Transition Metals – Ligand Substitution Reactions (A-Level Chemistry)

Transition Metals – Colour in Transition Metal Ions (A-Level Chemistry)

Transition Metals – Optical Isomerism in Complex Ions (A-Level Chemistry)

Transition Metals – Cis-Trans Isomerism in Complex Ions (A-Level Chemistry)

Transition Metals – Complex Ion Shape (A-Level Chemistry)

Transition Metals – Ligands (A-Level Chemistry)

Transition Metals – Introduction to Complex Ions (A-Level Chemistry)

CIE 3: Chemical bonding

Bonding – Hydrogen Bonding in Water (A-Level Chemistry)

Bonding – Forces Between Molecules (A-Level Chemistry)

Bonding – Bond Polarity (A-Level Chemistry)

Bonding – Molecular Shapes (A-Level Chemistry)

Bonding – Properties of Metallic Bonding (A-Level Chemistry)

Bonding – Covalent Bonds (A-Level Chemistry)

Bonding – Properties of Ionic Bonding (A-Level Chemistry)

CIE 30: Hydrocarbons

Aromatic Chemistry – Reactivity of Substituted Benzene (A-Level Chemistry)

Aromatic Chemistry – Friedel-Crafts Acylation and Alkylation (A-Level Chemistry)

Aromatic Chemistry – Halogenation Reactions in Benzene (A-Level Chemistry)

Aromatic Chemistry – Electrophilic Substitution Reactions in Benzene (A-Level Chemistry)

CIE 31: Halogen compounds

Aromatic Chemistry – Reactivity of Substituted Benzene (A-Level Chemistry)

Aromatic Chemistry – Electrophilic Substitution Reactions in Benzene (A-Level Chemistry)

CIE 32: Hydroxy compounds

Aromatic Chemistry – Reactivity of Substituted Benzene (A-Level Chemistry)

Carboxylic Acids and Derivatives – Acyl Groups (A-Level Chemistry)

CIE 33: Carboxylic acids and derivatives

Carboxylic Acids and Derivatives – Structure of Amides (A-Level Chemistry)

Carboxylic Acids and Derivatives – Acyl Groups (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Esters (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Carboxylic Acids (A-Level Chemistry)

CIE 34: Nitrogen compounds

Amino Acids, Proteins and DNA – Structure of Amino Acids (A-Level Chemistry)

Amines – Properties and Reactivity of Amines (A-Level Chemistry)

Amines – Amine Synthesis (A-Level Chemistry)

Amines – Introduction to Amines (A-Level Chemistry)

CIE 35: Polymerisation

Polymer Biodegradability (A-Level Chemistry)

Condensation Polymers (A-Level Chemistry)

Polyamide Formation (A-Level Chemistry)

CIE 36: Organic synthesis

Organic Synthesis – Organic Synthesis: Aromatic Compounds (A-Level Chemistry)

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

CIE 37: Analytic techniques

Analytical Techniques – Deuterium use in ¹H NMR (A-Level Chemistry)

Analytical Techniques – High Resolution ¹H NMR (A-Level Chemistry)

Analytical Techniques – Types of NMR: Hydrogen (A-Level Chemistry)

Analytical Techniques – Types of NMR: Carbon 13 (A-Level Chemistry)

Analytical Techniques – NMR Samples and Standards (A-Level Chemistry)

Analytical Techniques – Different Types of Chromatography (A-Level Chemistry)

Analytical Techniques – Chromatography (A-Level Chemistry)

CIE 4: States of matter

Bonding – Predicting Structures (A-Level Chemistry)

Bonding – Carbon Allotropes (A-Level Chemistry)

Bonding – Properties of Metallic Bonding (A-Level Chemistry)

Bonding – Properties of Covalent Structures (A-Level Chemistry)

Bonding – Properties of Ionic Bonding (A-Level Chemistry)

Amount of Substance – The Ideal Gas Equation (A-Level Chemistry)

CIE 5

CIE 6: Electrochemistry

Oxidation, Reduction and Redox Equations – Balancing Redox Equations (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Redox Processes (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Oxidation States (A-Level Chemistry)

CIE 7: Equilibria

Acids and Bases – Drawing pH Curves (A-Level Chemistry)

Acids and Bases – Acid-Base Indicators (A-Level Chemistry)

Acids and Bases – The pH Scale and Strong Acids (A-Level Chemistry)

Acids and Bases – Neutralisation Reactions (A-Level Chemistry)

Acids and Bases – Acid and Base Strength (A-Level Chemistry)

Acids and Bases – The Brønsted-Lowry Acid-Base Theory (A-Level Chemistry)

Equilibrium Constant for Homogenous Systems – Le Chatelier’s Principle in Gas Equilibria (A-Level Chemistry)

Equilibrium Constant for Homogenous Systems – Gas Equilibria and Kp (A-Level Chemistry)

Equilibrium Constant for Homogeneous System – Changing Kp (A-Level Chemistry)

Equilibrium Constant for Homogenous Systems – Gas Partial Pressures (A-Level Chemistry)

CIE 8: Reaction kinetics

Kinetics – The Maxwell–Boltzmann Distribution and Catalysts (A-Level Chemistry)

Kinetics – The Collision Theory and Reaction Rates (A-Level Chemistry)

CIE 9: The Periodic Table

Properties of Period 3 Elements – Properties of Period 3 Compounds (A-Level Chemistry)

Properties of Period 3 Elements – Reactivity of Period 3 Elements (A-Level Chemistry)

Periodicity – Trends Along Period 3 (A-Level Chemistry)

Periodicity – Classification (A-Level Chemistry)

CIE: 26: Reaction Kinetics, Catalysts

Transition Metals – Transition Metals as Homogeneous Catalysts (A-Level Chemistry)

Transition Metals – Transition Metals as Heterogeneous Catalysts (A-Level Chemistry)

Rate Equations – Reaction Determining Steps (A-Level Chemistry)

Rate Equations – Reaction Half Lives (A-Level Chemistry)

Rate Equations – Uses of Clock Reactions (A-Level Chemistry)

Rate Equations – Determining Orders of Reactions Graphically (A-Level Chemistry)

Rate Equations – Temperature Changes and the Rate Constant (A-Level Chemistry)

Rate Equations – The Rate Constant (A-Level Chemistry)

Rate Equations – Introduction to Orders of Reactions (A-Level Chemistry)

Rate Equations – The Rate Equation (A-Level Chemistry)

Edexcel Topic 1: Atomic Structure and the Periodic Table

Electrode Potentials and Electrochemical Cells – Electrode Potentials (A-Level Chemistry)

Periodicity – Trends Along Period 3 (A-Level Chemistry)

Ionisation Energies (A-Level Chemistry)

Periodicity – Classification (A-Level Chemistry)

Amount of Substance – Measuring Relative Masses (A-Level Chemistry)

Atomic Structure – Electron Arrangement (A-Level Chemistry)

Atomic Structure – Electrons in Atoms (A-Level Chemistry)

Atomic Structure – Mass Spectrometry (A-Level Chemistry)

Atomic Structure – Element Isotopes (A-Level Chemistry)

Atomic Structure – Atomic and Mass Number (A-Level Chemistry)

Edexcel Topic 10: Equlibrium 1

Calculations with Equilibrium Constants (A-Level Chemistry)

Chemical Equilibria applied to Industry (A-Level Chemistry)

Chemical Equilibria and Le Chatelier’s Principle (A-Level Chemistry)

Edexcel Topic 11: Equilibrium 2

Equilibrium Constant for Homogenous Systems – Le Chatelier’s Principle in Gas Equilibria (A-Level Chemistry)

Equilibrium Constant for Homogenous Systems – Gas Equilibria and Kp (A-Level Chemistry)

Equilibrium Constant for Homogenous Systems – Gas Partial Pressures (A-Level Chemistry)

Calculations with Equilibrium Constants (A-Level Chemistry)

Edexcel Topic 12: Acid-base Equilibria

Acids and Bases – Titrations (A-Level Chemistry)

Acids and Bases – Buffer Action (A-Level Chemistry)

Acids and Bases – Dilutions and pH (A-Level Chemistry)

Acids and Bases – pH of Strong Bases (A-Level Chemistry)

Acids and Bases – Ionic Product of Water (A-Level Chemistry)

Acids and Bases – The Acid Dissociation Constant, Ka (A-Level Chemistry)

Acids and Bases – Neutralisation Reactions (A-Level Chemistry)

Acids and Bases – Acid and Base Strength (A-Level Chemistry)

Acids and Bases – The Brønsted-Lowry Acid-Base Theory (A-Level Chemistry)

Edexcel Topic 13: Energetics 2

Thermodynamic – Calculations involving Free Energy (A-Level Chemistry)

Thermodynamic – Gibbs Free Energy (A-Level Chemistry)

Thermodynamic – Entropy Change Predictions (A-Level Chemistry)

Thermodynamic – Total Entropy Changes (A-Level Chemistry)

Thermodynamic – Introduction to Entropy (A-Level Chemistry)

Thermodynamic – Calculating Enthalpy Changes of Solution (A-Level Chemistry)

Thermodynamic – Enthalpy of Solution (A-Level Chemistry)

Thermodynamic – Enthalpy of Hydration (A-Level Chemistry)

Thermodynamic – Calculations involving Born-Haber Cycles (A-Level Chemistry)

Thermodynamic – Construction of Born-Haber Cycles (A-Level Chemistry)

Edexcel Topic 14: Redox 2

Transition Metals – Iodine-Sodium Thiosulfate Titrations (A-Level Chemistry)

Transition Metals – Carrying Titrations with Potassium Permanganate (A-Level Chemistry)

Transition Metals – Redox Potentials (A-Level Chemistry)

Transition Metals – Redox Reactions Revisited (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Commercial Applications of Fuel Cells (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Electrochemical Cells Reactions (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Representing Electrochemical Cells (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Electrode Potentials (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Half Cells and Full Cells (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Balancing Redox Equations (A-Level Chemistry)

Edexcel Topic 15: Transition Metals

Transition Metals – Autocatalysis of Transition Metals (A-Level Chemistry)

Transition Metals – Transition Metals as Homogeneous Catalysts (A-Level Chemistry)

Transition Metals – Transition Metals as Heterogeneous Catalysts (A-Level Chemistry)

Transition Metals – Examples of Redox Reactions in Transition Metals (A-Level Chemistry)

Transition Metals – Ligand Substitution Reactions (A-Level Chemistry)

Transition Metals – Colour in Transition Metal Ions (A-Level Chemistry)

Transition Metals – Optical Isomerism in Complex Ions (A-Level Chemistry)

Transition Metals – Cis-Trans Isomerism in Complex Ions (A-Level Chemistry)

Transition Metals – Complex Ion Shape (A-Level Chemistry)

Transition Metals – Ligands (A-Level Chemistry)

Edexcel Topic 16: Kinetics 2

Transition Metals – Autocatalysis of Transition Metals (A-Level Chemistry)

Transition Metals – Transition Metals as Homogeneous Catalysts (A-Level Chemistry)

Transition Metals – Transition Metals as Heterogeneous Catalysts (A-Level Chemistry)

Rate Equations – Reaction Determining Steps (A-Level Chemistry)

Rate Equations – Determining Orders of Reactions Graphically (A-Level Chemistry)

Rate Equations – Determining Order of Reaction Experimentally (A-Level Chemistry)

Rate Equations – Temperature Changes and the Rate Constant (A-Level Chemistry)

Rate Equations – The Rate Constant (A-Level Chemistry)

Rate Equations – Introduction to Orders of Reactions (A-Level Chemistry)

Rate Equations – The Rate Equation (A-Level Chemistry)

Edexcel Topic 17: Organic Chemistry 2

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Polymer Biodegradability (A-Level Chemistry)

Condensation Polymers (A-Level Chemistry)

Carboxylic Acids and Derivatives – Acyl Groups (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Esters (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Carboxylic Acids (A-Level Chemistry)

Aldehydes and Ketones – Testing for Carbonyl Compounds (A-Level Chemistry)

Aldehydes and Ketones – Reactivity of Carbonyl Compunds (A-Level Chemistry)

Aldehydes and Ketones – Carbonyl Compounds (A-Level Chemistry)

Optical Isomerism (A-Level Chemistry)

Edexcel Topic 18: Organic Chemistry 3

Organic Synthesis – Considerations in Organic Synthesis (A-Level Chemistry)

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Organic Synthesis – Practical Purification Techniques (A-Level Chemistry)

Organic Synthesis – Practical Preparation Techniques (A-Level Chemistry)

Amino Acids, Proteins and DNA – Structure of Proteins (A-Level Chemistry)

Amino Acids, Proteins and DNA – Structure of Amino Acids (A-Level Chemistry)

Polymer Biodegradability (A-Level Chemistry)

Polyamide Formation (A-Level Chemistry)

Condensation Polymers (A-Level Chemistry)

Amines – Properties and Reactivity of Amines (A-Level Chemistry)

Edexcel Topic 19: Modern Analytical Techniques 2

Analytical Techniques – High Resolution ¹H NMR (A-Level Chemistry)

Analytical Techniques – NMR Samples and Standards (A-Level Chemistry)

Analytical Techniques – Nuclear Magnetic Resonance Spectroscopy (A-Level Chemistry)

Analytical Techniques – Different Types of Chromatography (A-Level Chemistry)

Analytical Techniques – Chromatography (A-Level Chemistry)

Atomic Structure – Mass Spectrometry (A-Level Chemistry)

Edexcel Topic 2a & b: Bonding and Structure

Bonding – Hydrogen Bonding in Water (A-Level Chemistry)

Bonding – Forces Between Molecules (A-Level Chemistry)

Bonding – Bond Polarity (A-Level Chemistry)

Bonding – Molecular Shapes (A-Level Chemistry)

Bonding – Predicting Structures (A-Level Chemistry)

Bonding – Carbon Allotropes (A-Level Chemistry)

Bonding – Properties of Metallic Bonding (A-Level Chemistry)

Bonding – Properties of Covalent Structures (A-Level Chemistry)

Bonding – Properties of Ionic Bonding (A-Level Chemistry)

Edexcel Topic 3: Redox 1

Thermodynamic – Calculations involving Born-Haber Cycles (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Balancing Redox Equations (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Redox Processes (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Oxidation States (A-Level Chemistry)

Edexcel Topic 4: Inorganic Chemistry & The Periodic Table

Transition Metals – Redox Titrations (A-Level Chemistry)

Acids and Bases – Titrations (A-Level Chemistry)

The Halogens – Testing for Ions (A-Level Chemistry)

The Halogens -Halide Ions and their Reactions (A-Level Chemistry)

The Halogens – Disproportionation Reactions in Halogens (A-Level Chemistry)

The Halogens – Reactions with Halogens (A-Level Chemistry)

The Halogens – Group 7, The Halogens (A-Level Chemistry)

Uses of Group 2 Elements and their Compounds (A-Level Chemistry)

Reactions of Group 2 Elements (A-Level Chemistry)

Group 2, The Alkaline Earth Metals (A-Level Chemistry)

Edexcel Topic 5: Formulae, Equations and Amounts of Substance

Organic Synthesis – Considerations in Organic Synthesis (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Balancing Redox Equations (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Redox Processes (A-Level Chemistry)

Amount of Substance – Percentage Atom Economy (A-Level Chemistry)

Amount of Substance – Calculating Percentage Yields (A-Level Chemistry)

Amount of Substance – Stoichiometric Calculations (A-Level Chemistry)

Amount of Substance – Balancing Chemical Equations (A-Level Chemistry)

Amount of Substance – Empirical and Molecular Formulae (A-Level Chemistry)

Amount of Substance- The Mole and The Avogadro Constant (A-Level Chemistry)

Amount of Substance – The Ideal Gas Equation (A-Level Chemistry)

Edexcel Topic 6: Organic Chemistry 1

Organic Synthesis – Practical Purification Techniques (A-Level Chemistry)

Organic Synthesis – Practical Preparation Techniques (A-Level Chemistry)

Alcohols – Alcohol Reactivity (A-Level Chemistry)

Alcohols – Alcohol oxidation (A-Level Chemistry)

Alcohols – Introduction to Alcohols (A-Level Chemistry)

Alkenes – Addition Polymerisation in Alkenes (A-Level Chemistry)

Alkenes – Alkene Structure and Reactivity (A-Level Chemistry)

Halogenoalkanes – Reactivity of Halogenoalkanes (A-Level Chemistry)

Halogenoalkanes – Introduction to Halogenoalkanes (A-Level Chemistry)

Alkanes – Obtaining Alkanes (A-Level Chemistry)

Edexcel Topic 7: Modern Analytical Techniques 1

Organic Analysis – Infrared (IR) Spectroscopy (A-Level Chemistry)

Atomic Structure – Mass Spectrometry (A-Level Chemistry)

Edexcel Topic 8

Edexcel Topic 9: Kinetics 1

Kinetics – The Maxwell–Boltzmann Distribution and Catalysts (A-Level Chemistry)

Kinetics – The Collision Theory and Reaction Rates (A-Level Chemistry)

OCR 2.1.1 Atomic structure and Isotopes

Amount of Substance – Measuring Relative Masses (A-Level Chemistry)

Atomic Structure – Mass Spectrometry (A-Level Chemistry)

Atomic Structure – Element Isotopes (A-Level Chemistry)

Atomic Structure – Atomic and Mass Number (A-Level Chemistry)

OCR 2.1.2 Compounds, Formulae and Equations

Bonding – Ion Formation (A-Level Chemistry)

Amount of Substance – Balancing Chemical Equations (A-Level Chemistry)

OCR 2.1.3 Amount of Substance

Amount of Substance – Percentage Atom Economy (A-Level Chemistry)

Amount of Substance – Calculating Percentage Yields (A-Level Chemistry)

Amount of Substance – Empirical and Molecular Formulae (A-Level Chemistry)

Amount of Substance – Further Mole Calculations (A-Level Chemistry)

Amount of Substance- The Mole and The Avogadro Constant (A-Level Chemistry)

Amount of Substance – The Ideal Gas Equation (A-Level Chemistry)

OCR 2.1.4 Acids

Acids and Bases – Titrations (A-Level Chemistry)

Acids and Bases – Neutralisation Reactions (A-Level Chemistry)

Acids and Bases – The Brønsted-Lowry Acid-Base Theory (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Commercial Applications of Fuel Cells (A-Level Chemistry)

OCR 2.1.5 Redox

Oxidation, Reduction and Redox Equations – Redox Processes (A-Level Chemistry)

Oxidation, Reduction and Redox Equations – Oxidation States (A-Level Chemistry)

OCR 2.2.1 Electron structure

Atomic Structure – Electron Arrangement (A-Level Chemistry)

Atomic Structure – Electrons in Atoms (A-Level Chemistry)

OCR 2.2.2 Bonding and Structure

Bonding – Hydrogen Bonding in Water (A-Level Chemistry)

Bonding – Forces Between Molecules (A-Level Chemistry)

Bonding – Bond Polarity (A-Level Chemistry)

Bonding – Molecular Shapes (A-Level Chemistry)

Bonding – Properties of Covalent Structures (A-Level Chemistry)

Bonding – Covalent Bonds (A-Level Chemistry)

Bonding – Properties of Ionic Bonding (A-Level Chemistry)

OCR 3.1.1 Periodicity

Periodicity – Trends Along Period 3 (A-Level Chemistry)

Ionisation Energies (A-Level Chemistry)

Periodicity – Classification (A-Level Chemistry)

Bonding – Carbon Allotropes (A-Level Chemistry)

Bonding – Properties of Metallic Bonding (A-Level Chemistry)

OCR 3.1.2 Group 2

Uses of Group 2 Elements and their Compounds (A-Level Chemistry)

Reactions of Group 2 Elements (A-Level Chemistry)

Group 2, The Alkaline Earth Metals (A-Level Chemistry)

OCR 3.1.3 The Halogens

The Halogens -Halide Ions and their Reactions (A-Level Chemistry)

The Halogens – Disproportionation Reactions in Halogens (A-Level Chemistry)

The Halogens – Reactions with Halogens (A-Level Chemistry)

The Halogens – Group 7, The Halogens (A-Level Chemistry)

OCR 3.1.4 Qualitative analysis

The Halogens – Testing for Ions (A-Level Chemistry)

OCR 3.2.2 Reaction rates

Rate Equations – Measuring Rate of Reaction (A-Level Chemistry)

Kinetics – The Maxwell–Boltzmann Distribution and Catalysts (A-Level Chemistry)

Kinetics – The Collision Theory and Reaction Rates (A-Level Chemistry)

OCR 3.2.3 Chemical equilibrium

Calculations with Equilibrium Constants (A-Level Chemistry)

Chemical Equilibria applied to Industry (A-Level Chemistry)

Chemical Equilibria and Le Chatelier’s Principle (A-Level Chemistry)

OCR 4.1.1 Basic Concepts of Organic Chemistry

Introduction to Organic Chemistry – Structural Isomers (A-Level Chemistry)

Introduction to Organic Chemistry – Reaction Mechanisms in Organic Chemistry (A-Level Chemistry)

Introduction to Organic Chemistry – General Formulae (A-Level Chemistry)

Introduction to Organic Chemistry – Introduction to Functional Groups (A-Level Chemistry)

Introduction to Organic Chemistry – Naming and Representing Organic Compounds (A-Level Chemistry)

OCR 4.1.2 Alkanes

Alkanes – Alkanes: Properties and Reactivity (A-Level Chemistry)

OCR 4.1.3 Alkenes

Alkenes – Addition Polymerisation in Alkenes (A-Level Chemistry)

Alkenes – Alkene Structure and Reactivity (A-Level Chemistry)

Introduction to Organic Chemistry – E/Z Isomerism (A-Level Chemistry)

OCR 4.2.1 Alcohols

Alcohols – Alcohol Reactivity (A-Level Chemistry)

Alcohols – Alcohol oxidation (A-Level Chemistry)

Alcohols – Introduction to Alcohols (A-Level Chemistry)

OCR 4.2.2 Haloalkanes

Halogenoalkanes – Environmental Impact of Halogenalkanes (A-Level Chemistry)

Halogenoalkanes – Reactivity of Halogenoalkanes (A-Level Chemistry)

Halogenoalkanes – Introduction to Halogenoalkanes (A-Level Chemistry)

OCR 4.2.3 Organic synthesis

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Organic Synthesis – Practical Purification Techniques (A-Level Chemistry)

Organic Synthesis – Practical Preparation Techniques (A-Level Chemistry)

Organic Analysis – Identification of Functional Groups (A-Level Chemistry)

OCR 4.2.4 Analytical techniques

Organic Analysis – Infrared (IR) Spectroscopy (A-Level Chemistry)

Organic Analysis – Identification of Functional Groups (A-Level Chemistry)

Atomic Structure – Mass Spectrometry (A-Level Chemistry)

OCR 5.1.1 Rates, Equilibrium and pH

Rate Equations – Reaction Determining Steps (A-Level Chemistry)

Rate Equations – Reaction Half Lives (A-Level Chemistry)

Rate Equations – Uses of Clock Reactions (A-Level Chemistry)

Rate Equations – Determining Orders of Reactions Graphically (A-Level Chemistry)

Rate Equations – Determining Order of Reaction Experimentally (A-Level Chemistry)

Rate Equations – Temperature Changes and the Rate Constant (A-Level Chemistry)

Rate Equations – The Rate Constant (A-Level Chemistry)

Rate Equations – Introduction to Orders of Reactions (A-Level Chemistry)

Rate Equations – The Rate Equation (A-Level Chemistry)

OCR 5.1.2 How fast?

Equilibrium Constant for Homogenous Systems – Le Chatelier’s Principle in Gas Equilibria (A-Level Chemistry)

Equilibrium Constant for Homogenous Systems – Gas Equilibria and Kp (A-Level Chemistry)

Equilibrium Constant for Homogeneous System – Changing Kp (A-Level Chemistry)

Equilibrium Constant for Homogenous Systems – Gas Partial Pressures (A-Level Chemistry)

Calculations with Equilibrium Constants (A-Level Chemistry)

Chemical Equilibria applied to Industry (A-Level Chemistry)

Chemical Equilibria and Le Chatelier’s Principle (A-Level Chemistry)

OCR 5.1.3 Acids, Bases and Buffers

Acids and Bases – Acid-Base Indicators (A-Level Chemistry)

Acids and Bases – Titrations (A-Level Chemistry)

Acids and Bases – Buffer Action (A-Level Chemistry)

Acids and Bases – Dilutions and pH (A-Level Chemistry)

Acids and Bases – pH of Strong Bases (A-Level Chemistry)

Acids and Bases – Ionic Product of Water (A-Level Chemistry)

Acids and Bases – More Ka Calculations (A-Level Chemistry)

Acids and Bases – The Acid Dissociation Constant, Ka (A-Level Chemistry)

Acids and Bases – The pH Scale and Strong Acids (A-Level Chemistry)

Acids and Bases – Neutralisation Reactions (A-Level Chemistry)

OCR 5.2.1 Lattice enthalpy

Thermodynamic – Calculating Enthalpy Changes of Solution (A-Level Chemistry)

Thermodynamic – Enthalpy of Solution (A-Level Chemistry)

Thermodynamic – Calculations involving Born-Haber Cycles (A-Level Chemistry)

Thermodynamic – Construction of Born-Haber Cycles (A-Level Chemistry)

Thermodynamic – Enthalpy Key Terms (A-Level Chemistry)

Thermodynamic – Lattice Enthalpies (A-Level Chemistry)

OCR 5.2.2 Enthalpy and Entropy

Thermodynamic – Calculations involving Free Energy (A-Level Chemistry)

Thermodynamic – Gibbs Free Energy (A-Level Chemistry)

Thermodynamic – Total Entropy Changes (A-Level Chemistry)

Thermodynamic – Introduction to Entropy (A-Level Chemistry)

OCR 5.2.3 Redox and Electrode potentials

Transition Metals – Examples of Redox Reactions in Transition Metals (A-Level Chemistry)

Transition Metals – Iodine-Sodium Thiosulfate Titrations (A-Level Chemistry)

Transition Metals – Carrying Titrations with Potassium Permanganate (A-Level Chemistry)

Transition Metals – Redox Titrations (A-Level Chemistry)

Transition Metals – Redox Potentials (A-Level Chemistry)

Transition Metals – Redox Reactions Revisited (A-Level Chemistry)

Acids and Bases – Acid-Base Indicators (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Commercial Applications of Fuel Cells (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Electrochemical Cells Reactions (A-Level Chemistry)

Electrode Potentials and Electrochemical Cells – Electrode Potentials (A-Level Chemistry)

OCR 5.3.1 Transition elements

Precipitation Reactions of Metal Ions in Solution (A-Level Chemistry)

Transition Metals – Iodine-Sodium Thiosulfate Titrations (A-Level Chemistry)

Transition Metals – Carrying Titrations with Potassium Permanganate (A-Level Chemistry)

Transition Metals – Redox Titrations (A-Level Chemistry)

Transition Metals – Ligand Substitution Reactions (A-Level Chemistry)

Transition Metals – Colour in Transition Metal Ions (A-Level Chemistry)

Transition Metals – Optical Isomerism in Complex Ions (A-Level Chemistry)

Transition Metals – Cis-Trans Isomerism in Complex Ions (A-Level Chemistry)

Transition Metals – Complex Ion Shape (A-Level Chemistry)

Transition Metals – Ligands (A-Level Chemistry)

OCR 5.3.2 Qualitative analysis

Precipitation Reactions of Metal Ions in Solution (A-Level Chemistry)

OCR 6.1.1 Aromatic compounds

Aromatic Chemistry – Reactivity of Substituted Benzene (A-Level Chemistry)

Aromatic Chemistry – Friedel-Crafts Acylation and Alkylation (A-Level Chemistry)

Aromatic Chemistry – Halogenation Reactions in Benzene (A-Level Chemistry)

Aromatic Chemistry – Electrophilic Substitution Reactions in Benzene (A-Level Chemistry)

Aromatic Chemistry – Benzene Nomenclature (A-Level Chemistry)

Aromatic Chemistry – Improved Benzene Model (A-Level Chemistry)

Aromatic Chemistry – Introduction to Benzene (A-Level Chemistry)

OCR 6.1.2 Carbonyl compounds

Aldehydes and Ketones – Reactions to Increase Carbon Chain Length (A-Level Chemistry)

Aldehydes and Ketones – Testing for Carbonyl Compounds (A-Level Chemistry)

Aldehydes and Ketones – Reactivity of Carbonyl Compunds (A-Level Chemistry)

OCR 6.1.3 Carboxylic acids and Esters

Carboxylic Acids and Derivatives – Acyl Groups (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Esters (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Carboxylic Acids (A-Level Chemistry)

OCR 6.2.1 Amines

Amines – Introduction to Amines (A-Level Chemistry)

OCR 6.2.2 Amino acids, Amides and Chirality

Amino Acids, Proteins and DNA – Structure of Amino Acids (A-Level Chemistry)

Amines – Properties and Reactivity of Amines (A-Level Chemistry)

Amines – Amine Synthesis (A-Level Chemistry)

Carboxylic Acids and Derivatives – Structure of Amides (A-Level Chemistry)

Optical Isomerism (A-Level Chemistry)

OCR 6.2.3 Polyesters and Polyamides

Polymer Biodegradability (A-Level Chemistry)

Condensation Polymers (A-Level Chemistry)

Polyamide Formation (A-Level Chemistry)

OCR 6.2.4 Carbon–carbon Bond Formation

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Amines – Nitriles (A-Level Chemistry)

Amines – Amine Synthesis (A-Level Chemistry)

Aromatic Chemistry – Friedel-Crafts Acylation and Alkylation (A-Level Chemistry)

Carboxylic Acids and Derivatives – Acyl Groups (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Esters (A-Level Chemistry)

Carboxylic Acids and Derivatives – Properties and Reactivity of Carboxylic Acids (A-Level Chemistry)

Aldehydes and Ketones – Reactions to Increase Carbon Chain Length (A-Level Chemistry)

OCR 6.2.5 Organic synthesis

Organic Synthesis – Considerations in Organic Synthesis (A-Level Chemistry)

Organic Synthesis – Organic Synthesis: Aliphatic Compounds (A-Level Chemistry)

Organic Synthesis – Practical Purification Techniques (A-Level Chemistry)

Organic Synthesis – Practical Preparation Techniques (A-Level Chemistry)

OCR 6.3.1 Chromatography and Qualitative Analysis

Analytical Techniques – Different Types of Chromatography (A-Level Chemistry)

Analytical Techniques – Chromatography (A-Level Chemistry)

Organic Analysis – Identification of Functional Groups (A-Level Chemistry)

OCR 6.3.2 Spectroscopy

Analytical Techniques – Deuterium use in ¹H NMR (A-Level Chemistry)

Analytical Techniques – High Resolution ¹H NMR (A-Level Chemistry)

Analytical Techniques – Types of NMR: Hydrogen (A-Level Chemistry)

Analytical Techniques – Types of NMR: Carbon 13 (A-Level Chemistry)

Analytical Techniques – NMR Samples and Standards (A-Level Chemistry)

Analytical Techniques – Nuclear Magnetic Resonance Spectroscopy (A-Level Chemistry)