Rate Equations - Determining Order of Reaction Experimentally (A-Level Chemistry)
Determining Order of Reaction Expermentally
Using Data to determine the order
The Initial Rates Method
In the initial rate method, a series of experiments are conducted at constant temperature.
Each experiment is conducted at a different initial concentration of the reactant being investigated.
The concentration of all other reactants must be kept constant.
For each experiment, a graph is drawn of concentration vs time.
The gradient of the curve at the start of the reaction is calculated. This is the initial rate.
By comparing the initial rates at each concentration, the order of the reaction can be determined.
- Zero order – A change in concentration with no effect on the initial rate means that the reaction is zero order.
- First order – If the concentration is doubled and it is found that the initial rate also doubled, then the rate is first order.
- Second order – If the concentration is doubled, and the initial rate increases by a factor of four, then the reaction is second order.
Worked example: A series of experiments were conducted at constant temperature.
The initial rates were determined whilst the initial concentrations are changed.
The data is given below:
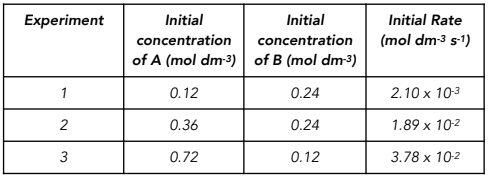
Use the data to determine the order of the reaction with respect to A, B and then determine the overall order
Answer:
Step 1: Find two experiments where the concentration of one reactant is constant
Consider reactions 1 and 2 where the concentration of B is constant.
Step 2: Determine the factor by which the concentration of the other reactant and rate changes. This gives the order.
The concentration of A increases by a factor of three.
The initial rate increases by a factor of nine.
Therefore the rate is second order with respect to A.
Step 3: Use two other experiments, and the order determined, to identify how the initial rate is expected to change.
Use investigations 2 and 3.
The concentration of A increases by a factor two.
We would expect the initial rate to increase by a factor of four.
Step 4: Determine the order of the other reactant by considering how the rate has actually changed.
The initial rate actually increases by a factor of two. So the change is a result of the change from the concentration of B.
The initial rate has decreased by a factor of 2.
From the data in the table, the concentration of B decreases by a factor of two.
Therefore the order of reaction with respect to B is first order.
The overall order of reaction is 2 + 1 = 3.






Still got a question? Leave a comment
Leave a comment