Atomic Structure - 4.2.3 Half-Lives and the Random Nature of Radioactive Decay (GCSE Physics AQA)

Half-Lives and the Random Nature of Radioactive Decay

Random Nature

• Radioactive decay is random. Although we can measure activity and count rate, we cannot predict which nucleus is going to decay at which time. This makes the nature of radioactive decay random.

Half-Life

• Half-life can be a measurement of decay. The half-life of a radioactive isotope can help us measure radioactive decay of a substance.

Half-life is defined as:

The time it takes for the number of nuclei of the isotope in a sample to halve.

OR

The time it takes for the count rate (or activity) from a sample containing the isotope to fall to half its initial level.

Calculating Half-Life

Question: The graph shows how the count rate from a sample containing the radioactive substance cobalt-60 changes with time.

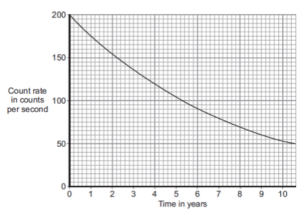
What is the half-life of cobalt-60?

1. To find the half life of cobalt-60, we need to know the definition of half life. Half life is the amount of time taken for the half the nuclei in the sample to decay, or for the count rate to halve.

2. On this graph, we are told about the count rate of the sample. The total count rate at the start is 200. To find half of this, we simply do 200 / 2 = 100. Therefore, half of the original count rate is 100.

3. To work out the half life, we simply need to find the value ‘100’ on the y axis of the graph. From this, we can simply read off the corresponding x axis value. This will be the value for the half life.

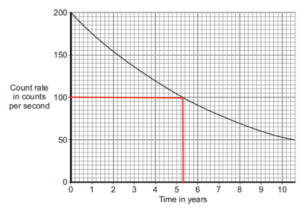
4. From this graph, we can see that the corresponding value is 5.3 years. This means that the half life of cobalt-60 is 5.3 years.

5. On the mark scheme, answers between 5.2 and 5.4 are accepted, but try to be as accurate as possible.

Calculating Decline in Emission

Question: The initial activity of a sample is 350 Bq. What is the final activity as a percentage of the initial activity after 2 half lives?

1. We need to work out the activity after 2 half lives.

After 1 half life, the activity is 350 / 2 = 175
After 2 half lives, the activity is 175 / 2 = 87.5

2. Now we must express the activity as a percentage of the original activity.

87.5 / 350 x 100 = 25 %
The final activity is 25% of the initial activity.