Forces - 5.7.2 Conservation of Momentum (GCSE Physics AQA)

Conservation of Momentum

Conservation of Momentum

Momentum is a very important concept in Physics, and it is a property of all moving objects.

There is a key principle that you should know in relation to this topic – the conservation of momentum:

In a closed system, the total momentum before an event is equal to the total momentum after the event.

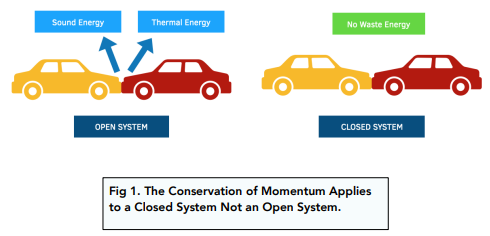
Closed and Open Systems

This principle is for a closed system. Remember, a closed system is one which does not exchange energy with the surroundings.

In real life, if there was a car crash, for example, it would be an open system so lots of energy would be lost as heat and sound energy to the surroundings. However, in AQA exams we will normally be assuming that it is a closed system to make calculations easier.

Examples of Momentum

Qualitative Scenarios of Momentum

Collisions are frequently used as examples of momentum in exam questions. Below we will practice some examples of momentum calculations.

Example Scenario: Imagine two skaters on an ice rink. Skater A is stationary, whilst Skater B is moving with a velocity. Skater B collides into Skater A, causing both skaters to move off together with a lower velocity. Momentum is conserved.

In this scenario, momentum has been conserved.

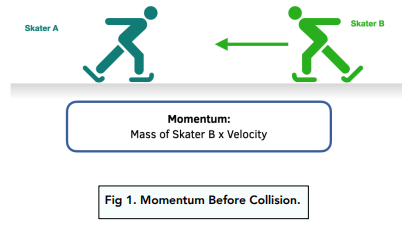
Momentum Before Collision

Before the two skaters collided, the momentum is: Mass of Skater B x Velocity. We do not take into account A, because it cannot have a momentum as it has a velocity of 0.

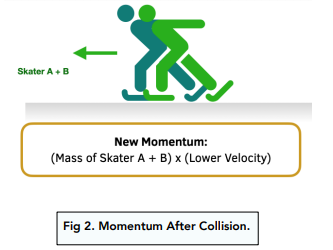
Momentum After Collision

After the collision, the momentum is: (Mass of A + B) x Velocity. The mass of the system will have increased because it is now (A + B) rather than just B. If momentum is to stay the same, the velocity must decrease.

Quantitative Scenarios of Momentum

In AQA exams, you may be asked to perform calculations involving momentum. We can elaborate on the previous example to demonstrate this.

Question: Imagine two skaters on an ice rink. Skater A (mass 45 kg) is stationary, whilst Skater B (mass of 60kg) is moving with a velocity of 6 m/s. Skater B collides into Skater A, causing both skaters to move off together with a lower velocity. Assuming that momentum is conserved, what is the new lower velocity, to 1 d.p.?

1. Draw a diagram.
The best way to start a momentum question is to draw a simple diagram.

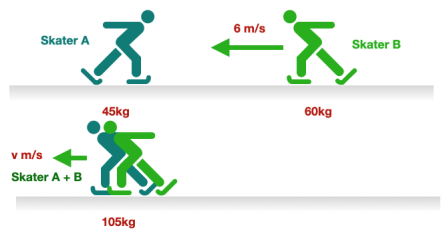
2. Calculate initial momentum.
This is the momentum before the collision occurs.

Initial momentum = mass x velocity
Initial momentum = 60 x 6
Initial momentum = 360 kg m/s

3. Calculate the final momentum.
We do not know the velocity, so we can substitute this with the symbol ‘v’.

Final momentum = mass x velocity
We need to calculate the total mass of both skaters when they move off together.
This is 45 + 60 = 105 kg.
Final momentum = 105 x v

4. Find ‘v’.
By using the concept of conservation of momentum, we know that the initial momentum = final momentum. We can use this to find ‘v’.

Initial momentum = Final momentum
360 = 105 x v
v = 360 / 105
v = 3.428571
v = 3.4 m/s (1dp)