Energy - 1.1.3 Changes in Energy (GCSE Physics AQA)

Changes in Energy

Calculating Energy Changes in Systems

Formula for Energy Change

We can calculate the amount of energy that is stored in or released from a system using this equation:

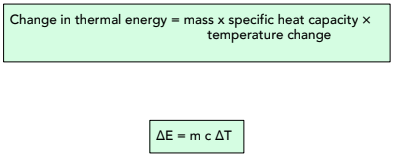
Where:

• change in thermal energy, ∆E, in joules, J
• mass, m, in kilograms, kg
• specific heat capacity, c, in joules per kilogram per degree Celsius, J/ kg°C
• temperature change, ∆T, in degrees Celsius, °C

We cannot just measure the rise in temperature to find out the change in thermal energy, because the amount of heat energy needed to increase the temperature by 1°C varies dependent on the mass and type of liquid:

• The mass is accounted for in the equation
• The type of liquid is accounted for in the specific heat capacity. We will look at this below.

Question: Louisa heats up a 20kg block of concrete. She waits until the temperature has risen from 20 °C to 65 °C. Find the energy used to heat up the block, given that the specific heat capacity of concrete is 3200 J/ kg°C.

1. We need to write out the equation for specific heat capacity.

∆E = m c ∆T

2. We need to calculate the temperature change.
We have not been told this value in the question, so we need to work it out.

65 – 20 = 45

3. We can use the formula.
We have all the numbers that we need, so we can simply substitute them into the formula. When we give our final answer, it may be more appropriate to give the units in terms of kilojoules.

∆E = m c ∆T
∆E = 20 x 45 x 3200 = 2 880 000 Joules
∆E = 2880 kJ

Question: Louisa heats up a 20kg block of concrete. She waits until the temperature has risen from 20 °C to 65 °C. Find the energy used to heat up the block, given that the s.h.c of concrete is 3200 J/kg°C.

1. Write out the equation for specific heat capacity.

Change in thermal energy = mass × specific heat capacity × temperature change

2. Calculate the temperature change.

∆T = 65°C – 20°C = 45°C

3. Use the formula.

∆T = 45°C
m = 20000 g
C = 3200 J/kg°C

∆E = 45 x 20000 x 3200 = 2880000 J
∆E = 2880 kJ

GCSE Physics Online Course

Covering every topic in the GCSE syllabus

Buy Now£29

Question: A student tried to measure the enthalpy change of combustion by burning 2.2g of liquid ethanol completely in oxygen. The amount of water used in the experiment was 100g and the temperature rose from 293K to 348K. The molar mass (Mr) of ethanol is 46.1. The specific heat capacity of water is 4.18 J g-1 K-1. What is the standard enthalpy change of combustion (∆c HƟ) of ethanol?

1. Write out the equation for specific heat capacity and fill in the values you know.

q = m C ∆T
q = ?
m = 100g
c = 4.18 J g-1 K-1
∆T = 348 – 293 = 55K

2. Calculate the heat energy transferred.

q = 100 x 4.18 x 55 = 22, 990 J

3. Convert the value of q into kJ.

q in kJ = 22, 990 ÷ 1000 = 22.9 kJ

4. Calculate the total number of moles of ethanol that burnt in the reaction.

Number of Moles = Mass of Substance / Mr
Mass of ethanol burnt = 2.2g
Mr = 46.1
Number of moles = 2.2/46.1 = 0.047722…

5. Calculate the standard enthalpy change of combustion.

∆ c HƟ = -22.9/ 0.047722 = -479.85909… = -480 kJ mol-1 (to 3 significant figures)

Specific Heat Capacity

When we calculated energy changes in the previous section, we used a value called ‘specific heat capacity’. For AQA exams, we need to know its definition.

The specific heat capacity of a substance is the amount of heat energy required to raise the temperature of one kilogram of the substance by one degree Celsius.

This is different for each liquid – e.g. it takes a different amount of heat energy to raise the temperature of water by 1°C compared to a different liquid.

If a large amount of energy is required to heat up a substance, then its specific heat capacity will be very high. These substances will be able to store lots of energy.

If a small amount of energy is required to heat up a substance, then its specific heat capacity will be very low. These substances won’t be able to store lots of energy.

Specific Heat Capacity of Water = 4200 J/kg°C

Investigating Specific Heat Capacity

Specific Heat Capacity of Liquid

Measuring the specific heat capacity of a liquid is fairly simple. We can heat up a liquid with a known amount of thermal energy, and then observe the temperature change caused.

We can re-arrange this:

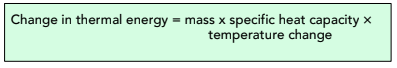
To:

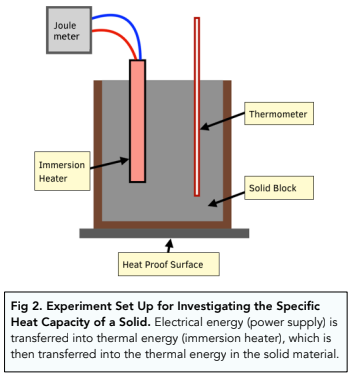
Specific Heat Capacity of Solid

We are able to calculate the specific heat capacity of a solid material too. Again, we want to heat up the solid with a known amount of thermal energy, and then observe the temperature change. You need to know a specific method for this experiment, so learn this well:

1. Take a block of material. First take the block that you are going to investigate. This block is going to have two things embedded into it: the thermometer to measure the temperature of the block, and the immersion heater to provide heat energy to the block. In this experiment we are essentially seeing how much heat energy is needed (from the immersion heater) to heat up the block by a certain temperature (measured by the thermometer).
2. Measure the mass of the block. You should measure the mass of the block using a top pan balance, recording the mass in kg.
3. Insulate the block. Insulate the block by coating it in an insulating material, such as a sponge or cotton wool. This will help to reduce the loss of heat to the surroundings.
4. Record the temperature of the block. We need to record the temperature of the block at the start of the experiment, in °C.
5. Attach the immersion heater to a joule-meter. The joule-meter will measure the amount of energy supplied to the block throughout the experiment.
6. Heat the block. Switch on the immersion heater and wait until the temperature of the block has risen by 10 degrees. The heater will provide thermal energy to the block, which we can measure using the joule-meter. We can measure the temperature of the block using the thermometer. Measure the final temperature of the block.
7. Find the energy and temperature change. Make a note of the final temperature change (which will be around 10 degrees) and the final energy value on the joulemter.
8. Rearrange the equation. Our equation for specific heat capacity is ∆E=mc∆T. In order to find the specific heat capacity of the block, we have to rearrange to make ‘c’ the subject of the formula (like we did earlier). Therefore, c = ∆E / m∆T.
9. Substitute in the numbers. Now that we have our equation, we can put in the values we have recorded. Our value of ∆E will be from the joule-meter, m is the mass of the block and ∆T is the temperature change that we measured.
10. Give the specific heat capacity in J/kg°C. Once we have calculated the value for specific heat capacity, we have to give the correct units, which is J/kg°C.