Stress, Strain, and Youngs Modulus

TensileStress & Strain

• An object can be deformed by opposing forces
• When forces cause an object to stretch, they are referred to as tensile forces
• Tensile forces give rise to two material properties, namely tensile stress and tensile strain

Tensile Stress

• Tensile stress is the force applied per unit area of a material’s cross-section

• Where:
  • σ = The symbol for tensile stress, measured in pascals (Pa)
  • F = represents the applied force in newtons (N)
  • A = is the cross-sectional area in square meters (m²)

• The ultimate tensile stress is the maximum force per original cross-sectional area that a wire can withstand before breaking
• The symbol σ is the Greek letter ‘sigma’
• The unit of measurement for σ is pascals (Pa), which is the same as pressure, which is also measured as force per unit area

Tensile Strain

• The extension per unit length is referred to as strain
• When a solid experiences stress, it undergoes deformation in the form of elongation or contraction, which is known as strain

• Where:
  • The increase in length of a solid is denoted by ΔL and measured in meters
  • The original length of a solid is represented by L and also measured in meters

• Strain is a dimensionless quantity as it is the ratio of lengths
• Sometimes, strain may be expressed as a percentage value
  • For example, if an object increases in length by 10% due to the application of a tensile or pulling force, it will exhibit a tensile strain value of +0.1 (the positive sign denotes that the strain is tensile as opposed to compressive)

Stress-Strain Curves

• The stress-strain curves provide information about the properties of materials, such as their brittleness, ductility, and the point at which they adhere to Hooke’s Law, and whether they exhibit elastic or plastic behavior
• The stress-strain curve for each material is unique

• The stress-strain graph contains critical points that bear resemblance to those found on the force-extension graph

• The stress-strain graph features several critical points that are distinct, including:
  • Yield Stress: This is the force per unit area at which a material undergoes plastic deformation without experiencing a significant increase in stress
  • The amount of elastic strain energy stored per unit volume can be determined by calculating the area beneath the linear Hooke’s Law section of the graph
  • Breaking point: The stress level at which a material fractures is referred to as the breaking stress. This is the maximum stress that a material can withstand before it fails
  • Elastic region: This section of the graph extends to the elastic limit. Within this range, a material will revert to its original form once the external force has been withdrawn
  • Plastic region: This section of the graph is situated beyond the elastic limit. Within this range, a material will experience permanent deformation and will not return to its original form once the external force has been withdrawn

In the case of small, reversible elastic strains, stress is directly proportional to strain, and the constant of proportionality for tensile and compressive stress is known as Young’s modulus, denoted as EY:

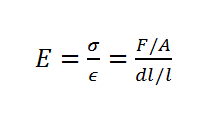
Young’s modulus serves as a measure of a material’s stiffness, and it is not dependent on the object’s shape or size. The value of Young’s modulus varies across real materials, ranging from approximately 10 MPa (for foam or rubber) to approximately 100 GPa (for ceramics and metals).

A. Tensile Stress

When a wire or a spring is elongated, a tensile force is exerted on it. The tensile stress, σ, is the amount of force per unit area of cross-section. The SI units of tensile stress are N m^-2.

Calculation of Tensile Stress

Tensile stress can be computed using experimental data. For example, let us consider an iron rod with a cross-sectional area (A) of 2 m^2. A tensile force (F) of 500 N is applied to both ends of the rod, as depicted in Figure 1.

B. Tensile Strai

When a wire or a spring is stretched, a tensile force is exerted on it. The amount of extension per unit length of the material is referred to as tensile strain (ε). Since it is a ratio of two lengths, tensile strain does not have any units.

Calculation of Tensile Strain

Tensile strain can be determined using experimental data. Let us assume a 2 m-long iron rod subjected to a tensile force that stretches it by 0.02 m, as depicted in Figure 2.

C. Elastic Strain Energy

When an object is subjected to a force that changes its shape within the elastic limit, the object can perform work as it returns to its original shape upon removal of the force. The potential energy stored in the material as it undergoes deformation is known as elastic strain energy.

Calculation of Elastic Strain Energy

Elastic strain energy can be determined using a graph of force (F) versus extension (e). The elastic strain energy is equal to the area under the curve, as illustrated in Figure 3.

D. Breaking Stress

The breaking stress, also referred to as the tensile strength, of a material is the maximum tensile stress that it can withstand before breaking. Figure 4 depicts the breaking stress on a stress-strain graph.

E. Plastic Deformation

Beyond the elastic limit, materials cease to follow Hooke’s Law, and any further deformation becomes permanent, known as plastic deformation. The proportionality limit (P) and elastic limit (E) are illustrated in the stress-strain graph below.

F. Brittle Failure

A material that breaks with little or no deformation is known as brittle, while materials that can withstand deformation before breaking are classified as ductile.

G. Practical Applications of Stress and Strain:

The mechanical properties of stress, strain, and plastic deformation are utilized in the design of various machine components such as gears, chains, and columns.

H. Summary

Properties such as tensile stress, tensile strain, strain energy, breaking stress, elastic and plastic deformations, and brittle failure are essential for understanding a material’s behavior and are widely utilized in machine component design.

• Tensile stress (σ) is defined as the force per unit area of cross-section.
• Tensile strain (ε) is the extension per unit length of a material.
• Elastic strain energy is the potential energy stored in a body due to deformation.
• The breaking stress is the tensile stress at which a material fails.
• Plastic deformation refers to any deformation that occurs beyond the elastic limit.
• Brittle failure describes a material failure that occurs with little or no deformation, typically seen in metals.

Young’s Modulus

Young’s Modulus is a measure of the stiffness of a material, and describes how much strain a material will undergo (i.e. how much it will stretch) as a result of a given amount of stress. The Young’s Modulus E of a material is calculated as:

The values for stress and strain must be taken at as low a stress level as possible, provided a difference in the length of the sample can be measured. Strain has no units due to simply being the ratio between the extension and original length of a material, so Young’s Modulus is measured by the same units as stress, i.e. newtons per square metre (Nm^-2) or Pascals (Pa). As Young’s Modulus is measured per unit area, it is an intensive property, meaning it only depends on the material being used, and not on the size of the material.