What exactly do Electromotive Force and Internal Resistance refer to?

What is Electromotive Force?

emf = ΔE/Δq

The equation expresses the relationship between electromotive force (EMF) measured in volts (V), the change in energy measured in Joules (J), and the change in charge measured in Coulombs (C), denoted as ΔE and Δq respectively.

Electromotive force, despite its name, does not act like a force in the conventional sense. Instead, it denotes the amount of energy per unit of charge supplied by a power source to facilitate the flow of electric charges within a circuit. The concept is akin to fluid pressure, which represents the energy per unit of volume available to displace a fluid.

Several factors can impact the electromotive force (EMF) of a power source, including the chemical properties of the materials utilized in the battery, the temperature of the battery, and external circumstances like the resistance of the circuit. Moreover, the EMF of a power source may fluctuate over time as the chemical reactions that generate the energy can become depleted or otherwise modified.

It is crucial to recognize that the electromotive force (EMF) of a power source does not correspond to the actual voltage observed across the circuit. Rather, it represents the maximum voltage that could be achieved in an ideal circuit devoid of internal resistance. In practice, the measured voltage across the circuit will be lower than the EMF due to the presence of internal resistance in the power supply and the circuit.

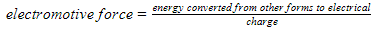
What is Internal Resistance?

During the transmission of current from a power source to a circuit, a portion of the electrical energy is dissipated due to the internal resistance of the power source. This internal resistance induces a voltage reduction across the power source, leading to the conversion of some electrical energy into heat. As a result, the power source may experience a rise in temperature, especially if it is supplying a substantial amount of current.

The quantity of heat produced by a power source is contingent on both its internal resistance and the magnitude of the current it is supplying. Typically, power sources that exhibit lower internal resistance will release less energy as heat and, as a consequence, generate lower levels of heat when delivering a specific amount of current.

When designing circuits or choosing power sources, it is critical to factor in the heat produced by the power supply, particularly in scenarios where it is expected to provide a high current output for a prolonged duration. Overheating can cause harm to the power source and other elements of the circuit, posing a safety risk as well.

Take a look at Figure 1 provided below, which illustrates a circuit consisting of a power supply that has an emf (E) and internal resistance (r). An external resistor (R), also known as a load, is connected in series. The circuit has a current (I) flowing through it, and the voltage across the resistor (R) is referred to as VR, while the voltage across the internal resistance (r) is known as Vr.

Applying the principle of conservation of energy,

E = VY + VR

it follows that the potential across the load – known as the terminal potential difference –

VR = E – VY

is equivalent to the potential difference across the power supply’s terminals (V) during current delivery, measured in volts (V). As current passes through the power supply, a portion of electrical energy is dissipated due to its internal resistance, resulting in a voltage decrease across the power supply – known as lost volts (VL) – which equals the product of the power supply’s internal resistance (r) and the current (I):

VL = I x r

Consequently, the terminal potential difference is lower than the power supply’s electromotive force (emf), which is the highest possible voltage that the power supply could generate in an ideal circuit without internal resistance. The discrepancy between the emf and the terminal potential difference corresponds to the lost volts:

emf – V = VL

Lost volts indicate the energy that dissipates as heat due to the power supply’s internal resistance, and they can substantially affect circuit performance. It may be necessary to decrease the power supply’s internal resistance or incorporate external components, like voltage regulators, to sustain the desired terminal potential difference in certain situations.

lost volts = electromotive force – terminal potential difference

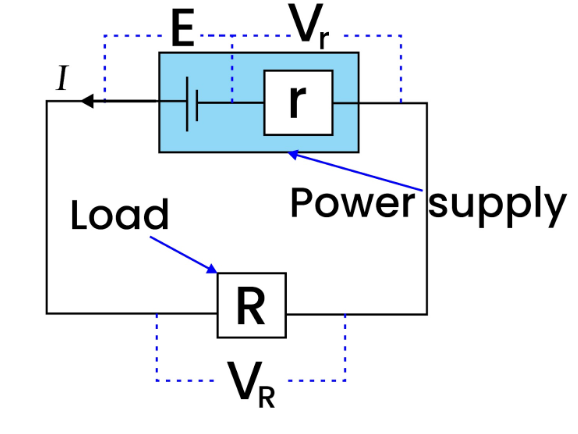
When the cell is in an open circuit (with no current flow), the terminal potential difference corresponds to the electromotive force. To measure the emf, a high-resistance voltmeter can be linked across the cell’s terminals, as illustrated in Figure 2.

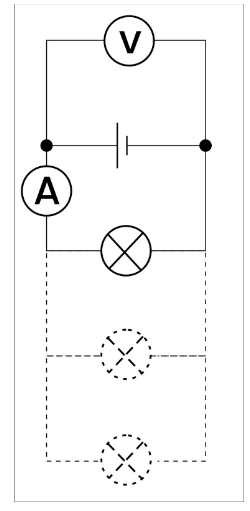
By employing this circuit, one can demonstrate that the power supply’s terminal potential difference decreases as the delivered current intensifies. When more lamps are linked across the cell, the current surges. The lost volts are provided by the following expression:

lost volts = current x internal resistance

With an increase in current, the lost voltage also rises, causing a decrease in the terminal potential difference.

According to Figure 1, the emf can be written as:

E = Ir + IR = I(r + R)

As observed in the previous equation, it is apparent that the power supply provides the maximum current when connected to a load with a negligible resistance (R=0). In this scenario, the terminal potential difference is zero since the potential difference across the power supply’s internal resistance equals the cell’s emf.

How does the internal resistance impact a battery?

The circuit illustrated below provides the formula for the power supplied by a battery to a load resistor with adjustable resistance.

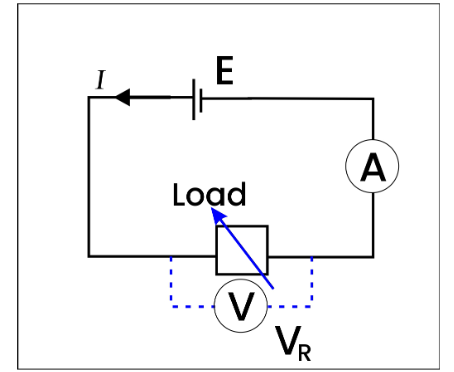
Current and voltage readings are obtained from the ammeter and voltmeter, respectively, for various resistance values. The resistance is computed using the equation . The power is then determined using the formula The graph below demonstrates how the power dispersed varies with respect to the load resistance. It is evident from this plot that the maximum power is supplied at a specific load value, which corresponds to the cell’s internal resistance.

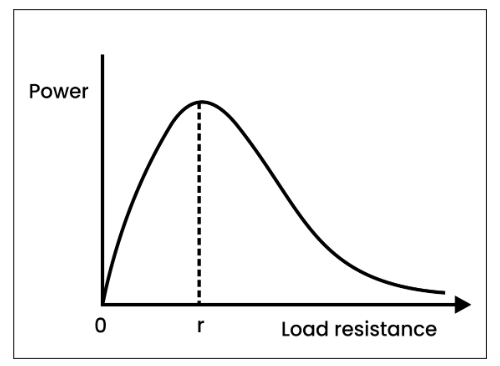
The load resistance that matches the battery’s internal resistance results in the battery supplying maximum power to the circuit.