Uniform and Electric Fields

Electric Field Definition

• When an electric charge “experiences” a force, it is said to be within an electric field
• The electric field strength is the measure of:

the electrostatic force per unit positive charge exerted on a stationary point charge at a specific location

• To calculate the electric field strength, one can use the following equation:

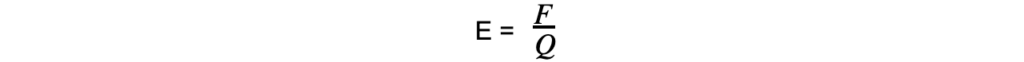
• Where:
  • E = represents the electric field strength (measured in N C-1)
  • F = is the electrostatic force on the charge (measured in N)
  • Q = represents the charge (measured in C)
• It’s crucial to use a positive test charge when defining electric field strength because it determines the direction of the electric field
• Electric field strength is a vector quantity and is always directed:
  • away from a positive charge,
  • while it is directed towards a negative charge
• It’s worth noting that opposite charges (positive and negative) attract each other
• While like charges (positive and positive or negative and negative) repel each other

Forces on Charges

• One can rearrange the electric field strength equation to solve for the force F exerted on a charge Q within an electric field E:

F = QE

• The following variables are used in this equation:
  • F = represents the electrostatic force on the charge, measured in N
  • Q = represents the charge, measured in C
  • E = represents the electric field strength, measured in N C-1
• The direction of the force exerted on the charge is dependent on the type of charge:
  • If the charge is positive (+), the force is exerted in the same direction as the electric field (E)
  • If the charge is negative (–), the force is exerted in the opposite direction to the electric field (E)

The force exerted on the charge will cause it to accelerate if it is in the same direction as the electric field (E), or decelerate if it is in the opposite direction

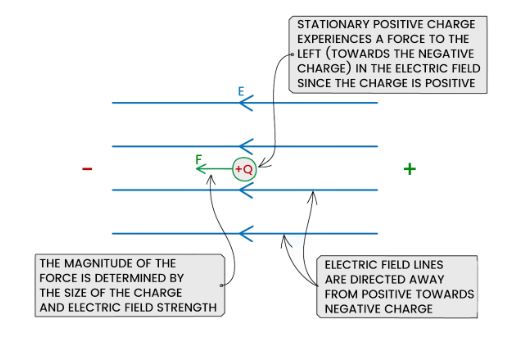
• Note: It should be noted that the force acting on a charge will always be parallel to the electric field lines

Point Charge Approximation

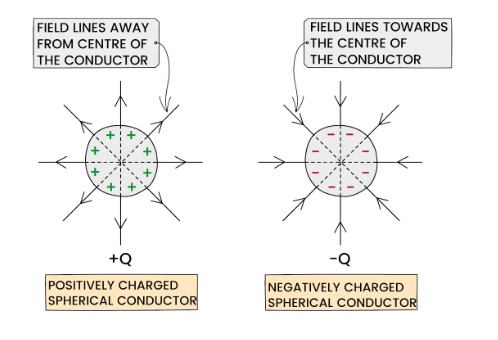
• When considering a point outside a spherical conductor, the charge of the conductor can be treated as a point charge located at its center
  • A spherical conductor is said to be uniform when its charge is evenly distributed
• Consequently, the electric field lines around a spherical conductor are identical to those around a point charge
• An example of a spherical conductor is a charged sphere
• The electric field lines around a spherical conductor are radial and their direction is determined by the charge of the sphere
  • If the spherical conductor is positively charged, the electric field lines are directed away from the center of the sphere
  • Conversely, if the spherical conductor is negatively charged, the electric field lines are directed towards the center of the sphere

Representing Electric Fields

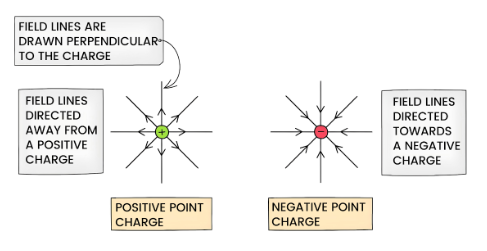
• The direction of electric fields can be represented by electric field lines
• Electric field lines point from positive to negative charges
  • Therefore, the field lines must extend away from the positive charge and towards the negative charge
• A radial field emanates uniformly from a charge in all directions, as observed in the field around a point charge or a sphere
  • e.g. the field around a point charge or sphere, The field lines extend outward in all directions from a positive point charge or inward toward a negative point charge.
• In the case of a point charge, the electric field lines are oriented directly radially inwards or outwards.:
  • For a positive (+) charge, the field lines extend radially outwards
  • In contrast, for a negative (-) charge, the field lines are directed radially inwards

• This concept is similar to radial gravitational field lines surrounding a point mass
• However, gravity is solely an attractive force, so the field lines will resemble those of a negative charge, whereas electric field lines may go in either direction

• A uniform electric field has an identical electric field strength throughout the entire field
  • For instance, the field between parallel plates with opposite charges
• This is depicted by evenly spaced field lines
  • Uniform gravitational field lines on the surface of a planet share similarities with this

• In contrast, a non-uniform electric field has varying electric field strength throughout
• The field line spacing determines the electric field strength:
  • The field lines are closer together in a stronger field
  • Conversely, field lines farther apart indicate a weaker field

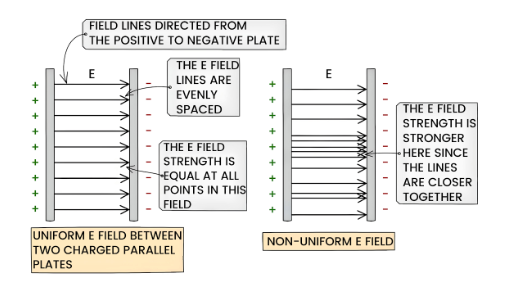
• The direction of the electric field lines between the parallel plates is from the positive plate to the negative plate
• A radial field, on the other hand, is non-uniform, as the electric field strength E varies depending on the distance from the charged particle
  • Therefore, the electric field strength E is not constant and changes as you move further away from or closer to the charged particle

Electric Field Strength

• The electric field strength between two charged parallel plates can be calculated using the following equation:

• Where:
  • E = electric field strength (V m-1)
  • ΔV = potential difference between the plates (V)
  • Δd = separation between the plates (m)
• It is important to note that the electric field strength is now measured in units of       V m-1
• The equation shows:
  • that the strength of the field is directly proportional to the potential difference
  • between the plates and inversely proportional to the separation distance
• However, this equation is not applicable for calculating the electric field strength around a point charge as it creates a radial field
• The electric field is directed from the plate connected to the positive terminal of the cell towards the plate connected to the negative terminal

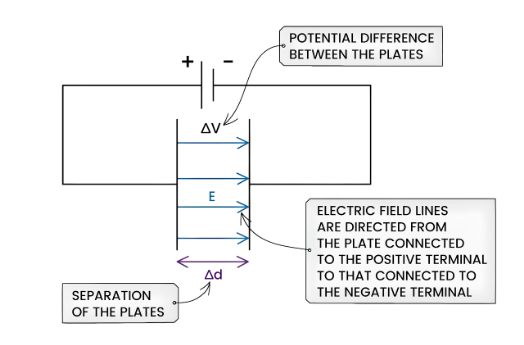
• Note: In case one of the parallel plates is grounded, its voltage is 0 V

Calculation of Electric Field Strength Due to a Point Charge

• At a given point, the electric field strength represents the intensity of an electric field
• The electric field strength (E) at distance (r) from a point charge (Q) in a vacuum is determined by the formula:

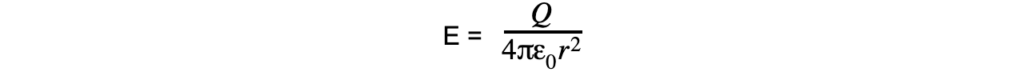
• Where:
  • Q = represents the electric charge generating the field (Coulomb)
  • r = is the distance from the center of the charge (meter)
  • ε0 = is the permittivity of free space (Farad/meter) (F m-1)
• This equation indicates that:
  • The electric field strength is not constant and varies with distance
  • The strength of the electric field decreases by a factor of 1/r² as the distance from the charge increases
• This relationship follows an inverse square law
• Hence, the field strength drops by a factor of four if the distance is doubled
• This formula is only applicable to radial fields produced by point charges
• The direction of the electric field strength is the same as that of the electric field lines
  • If the charge is negative, the field strength is negative and points toward the charge’s center
  • If the charge is positive, the field strength is positive and points away from the charge’s center
• This formula is similar to that used to determine the gravitational field strength around a point mass