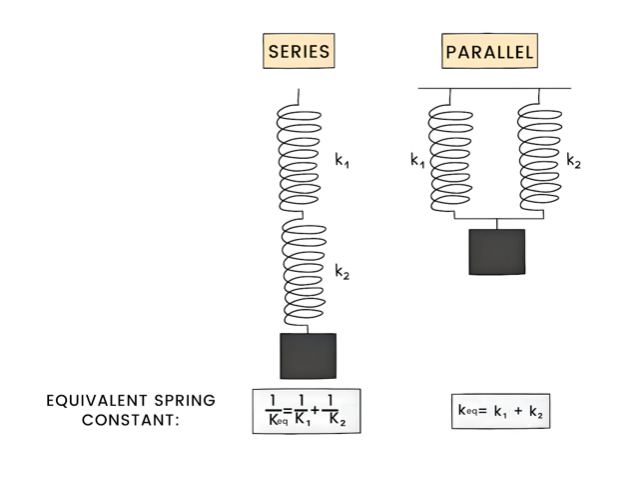
Springs
SUMMARY
- Deformation refers to changes in the size or shape of an object, which are caused by a deforming force.
- A material that can return to its original size and shape after a deforming force is applied and then removed is considered elastic. Steel is an example of such a material.
- A material that undergoes permanent deformation after a deforming force is applied and then removed is considered plastic. Wet clay is an example of such a material.
- If a material is prone to fracturing under a deforming force, it is classified as brittle. Concrete is an example of a brittle material.
- As long as the deforming force remains below the elastic limit for a given material, all solid materials can be considered elastic.
- Theterm “spring” refers to…
- a device that operates based on its elasticity.
- a constituent of a machine that serves to exert a predetermined force or accumulate energy.
- commonly crafted from steel that has been coiled.
- Inrelation to springs, Hooke’s law…
- establishes that the amount of force required to deform a spring is directly proportional to the extent of its deformation, expressed as a change in length (∆x).
F ∝ ∆x
- This relationship can be mathematically represented by the equation:
F = −k∆x.
- Where,
- The variable denoted by “k“…
- is referred to as the spring constant due to its variability among different springs.
- Its SI unit is newton per meter [N/m]
- although variants such as newton per centimeter [N/cm] or newton per millimeter [N/mm] are also frequently used
- The variable denoted by “k“…
- The expression ∆x = x − x0 represents…
- the difference between the spring’s current length x and its original length x0, which is also known as its relaxed length or equilibrium length.
- When x > x0, ∆x is considered an extension or elongation of the spring.
- Conversely, when x < x0, ∆x is regarded as a compression or contraction of the spring.
- The negative sign in the equation F = −k∆x indicates…
- that the force exerted by the spring acts in the opposite direction to the change in length.
- Specifically, this negative sign indicates that the spring generates a restoring force that seeks to return the spring to its equilibrium length.
- Hooke’s law is a fairly accurate model for numerous springs and other elastic materials within a certain range of force and length changes.
- If a spring adheres to Hooke’s law, its elastic potential energy (Us) can be calculated using the formula:
Us = ½k∆x2
In A-Level Physics, a spring is a type of elastic material that can be stretched or compressed when a force is applied. It is commonly used as a simple model for studying the behavior of other elastic materials.
Hooke’s law states that the force needed to stretch or compress a spring is directly proportional to the displacement of the spring from its equilibrium position. This law is particularly relevant to springs in A-Level Physics, as it helps to predict the behavior of a spring when a force is applied.
The spring constant is a measure of the stiffness of a spring. It is denoted by the symbol k and is directly proportional to the force needed to stretch or compress a spring by a certain distance. The relationship between the spring constant and Hooke’s law is that the force needed to stretch or compress a spring is equal to the spring constant multiplied by the displacement of the spring from its equilibrium position.
Simple harmonic motion is a type of periodic motion where the restoring force is directly proportional to the displacement from equilibrium. It is a common type of motion observed in systems involving springs, such as a mass attached to a spring. The behavior of a spring under simple harmonic motion can be described using equations that relate the spring constant, the mass, and the displacement of the mass from equilibrium.
The period of oscillation for a mass-spring system can be calculated using the equation T=2π√(m/k), where T is the period in seconds, m is the mass of the object attached to the spring in kilograms, and k is the spring constant in N/m.
Springs are often used as a simple model for studying the behavior of other elastic materials, such as rubber bands or metal wires. By analyzing the behavior of a spring under different forces and conditions, you can gain insights into the behavior of other elastic materials.
Springs have many real-world applications, such as in shock absorbers, suspension systems, and door hinges. By understanding the behavior of springs and the factors that affect their performance, you can apply this knowledge to design and optimize these types of systems.





Still got a question? Leave a comment
Leave a comment