Refraction and Internal Reflection
Total Internal Reflection
Critical Angle
The Critical Angle (co) refers to the angle of incidence in a dense medium, which causes the angle of refraction in the less dense medium to be 90o.
When observing the diagrams (provided below), it can be noted that as the angle of incidence in the dense medium increases, the angle of refraction gradually moves towards 90o. Simultaneously, a faint reflected ray can also be observed.
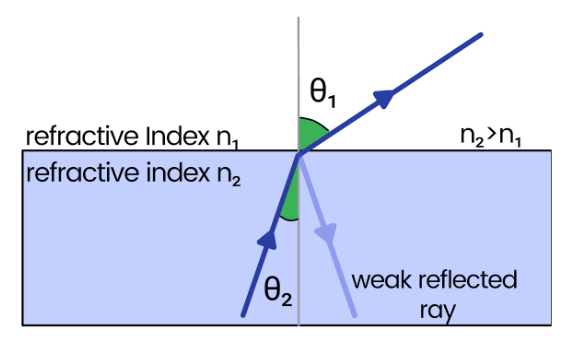
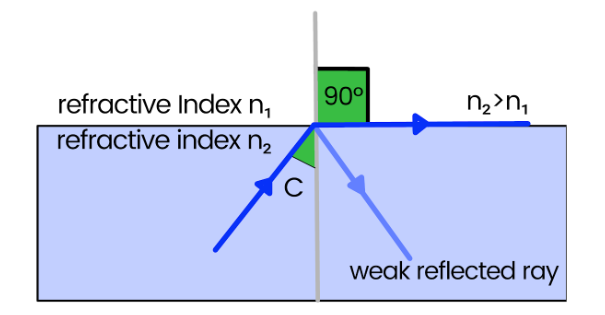
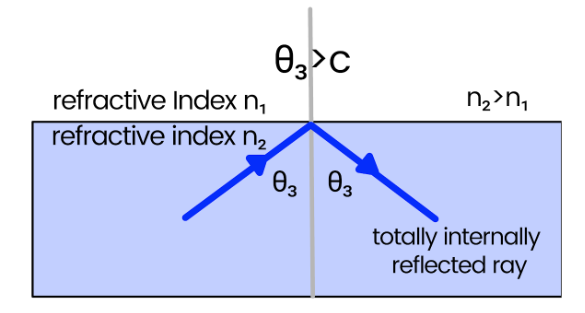
Snell’s Law can be utilized to derive an equation for the Critical Angle between two media of refractive index n1 & n2 .
sin1sin2 = n2n1
n1sin1 = n2sin2
The equation is derived for the scenario when θ1= 90o and θ2= co
n1sin(90o) = n2sin(c)
As sin(90o) = 1, this implies that
n1 = n2sin(c)
sin(c) = n1n2
based on the principles of relative refractive index,
n2n1 = 1n2 n1n2 = 11n2
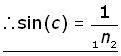
A deviation of 90o achieved using a prism with a 90o angle.
The occurrence of total internal reflection in glass is reliant on its critical angle, which is roughly 42o. Any light ray with an angle of incidence greater than this value will undergo total internal reflection. Hence, if a light ray enters at an angle of incidence of 45o, it will be reflected internally and will exit the glass prism at an angle of reflection of 45o, resulting in a total deviation of 90o.
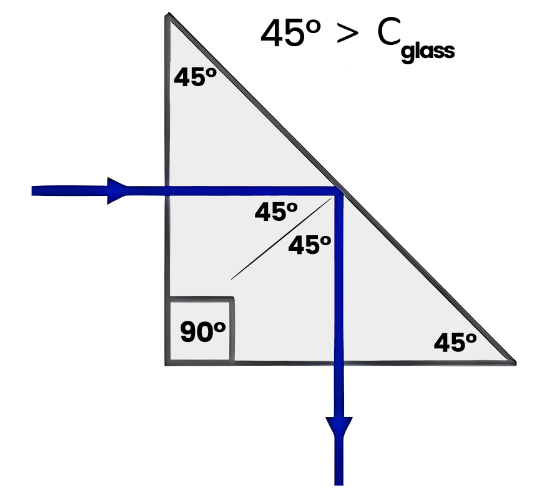
To achieve a 90o deviation, a 90o isosceles glass prism is employed. This enables both the incident ray and the reflected rays to enter and leave the prism’s surfaces normally, thus ensuring an unimpeded path. The hypotenuse of the prism is responsible for total internal reflection
A 90o prism can achieve a deviation of 180o
In addition to a 90o deviation, an isosceles prism can also create a 180o deviation, whereby reflection occurs on the equal, adjacent sides of the prism, rather than on the hypotenuse
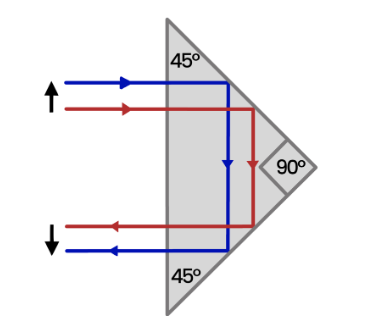
By following the path of two light rays through the prism, it becomes apparent that the resulting image is inverted. However, due to the image being reflected twice, lateral inversion is eliminated.
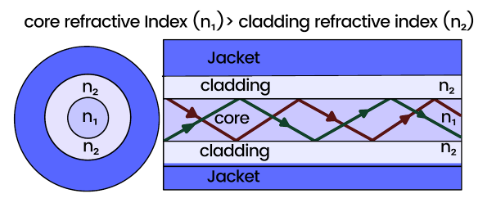
Optical fibers
Optical fibers are composed of a high refractive index core that is surrounded by a cladding material with a lower refractive index. As light travels through the fiber, it undergoes total internal reflection at the interface between these two media.
Refraction
Refraction occurs when waves cross the boundary between two materials, causing a change in speed.
If the wave is at an angle other than the normal line, it also undergoes a change in direction.
The degree of change in speed is quantified by the material’s refractive index, denoted by n. It is computed as the ratio of the speed of light in a vacuum (cv) to the speed of light in the given material (cm).
n is given by: n = cv / cm
where cv is the speed of light in a vacuum, and cm the speed of light in the material in question. n is unitless.
The refractive index between two materials is expressed as: 1n2
This value is the ratio of the speed of light in material 1 to that in material 2, given by c1/c2:
1n2 = c1/c2 = n1/n2
According to Snell’s Law, the ratio of the sines of the angles of incidence and refraction is equivalent to the ratio of the refractive indices of the two materials:
sini /sinr = c1/c2 = 1n2
By knowing the refractive index of the two materials, the angle of refraction can be determined using Snell’s Law. Additionally, the refractive index can be computed by measuring the angles of the light in the materials and calculating the sine of those angles.
Refraction
Introduction
Refraction occurs when a wave changes direction due to a change in speed as it travels from one medium to another. This phenomenon can be observed when light travels from air to glass or when water waves move from deeper to shallower water.
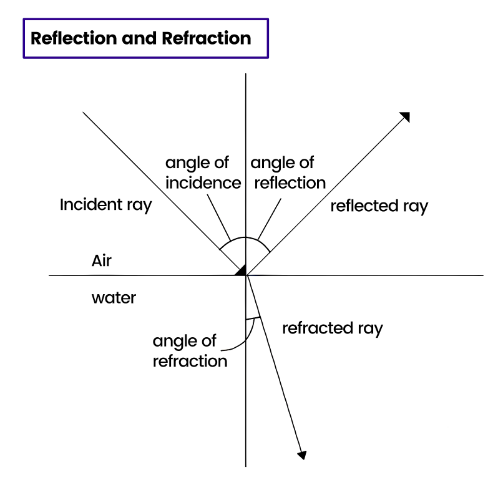
A. Refraction
Figure 1 illustrates the refraction of light as it moves from air to glass. The normal ray is perpendicular to the barrier, while the incident ray forms an angle with the normal known as the angle of incidence (i). The light ray bends as it enters the glass due to the change in speed, and the resulting refracted ray forms an angle with the normal known as the angle of refraction (r).
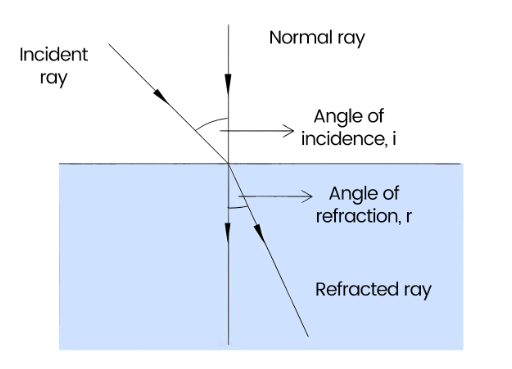
B. Refractive Index
Through various experiments, a direct relationship has been discovered between the angle of incidence and angle of refraction. This relationship is known as Snell’s law and is represented mathematically by the equation below.
sin isin r = a constant
The constant denoting the refractive index is typically represented by the letter “n”. Subscripts are commonly used to indicate the initial and final media through which the wave travels. When a wave moves from medium 1 to medium 2, Snell’s law can be expressed as follows,
sin isin r = n21
The table below illustrates the refractive index of various substances.
| Material | Refractive index |
| Crown glass | 1.52 |
| Diamond | 2.42 |
| Liquid water | 1.33 |
| Ice | 1.31 |
| Air | 1.0003 |
| Benzene | 1.50 |
C. Wave Speed and Refraction
Refraction is a result of a change in wave speed, and the degree of refraction is dependent on the extent of this speed change. The refractive index is a measure of the degree to which a ray bends as it transitions from one medium to another. Additionally, the refractive index is equal to the ratio of the speeds of the wave in the two media.
n21 = sin isin r = speed in medium 1speed in medium 2 = v1v2
The refractive index for rays transitioning from medium 2 to medium 1 can be expressed mathematically as,
n12 = v2v1 = 1n21
D. Total Internal Reflection
As light rays pass from a more optically dense medium to a less dense medium, they are refracted away from the normal due to the increased speed of light. This effect can be explored through experimentation with a semi-circular block, where measurements of angles inside and outside of the block can be taken from the flat side.
When the angle of incidence within the glass block is gradually increased, the corresponding angle of refraction also increases and exceeds the angle within the block. However, once the internal angle surpasses a certain value, the ray no longer leaves the glass and instead reflects within, following the law of reflection. In such cases, there is no refraction and the ray experiences total internal reflection, as illustrated in Figure 2.
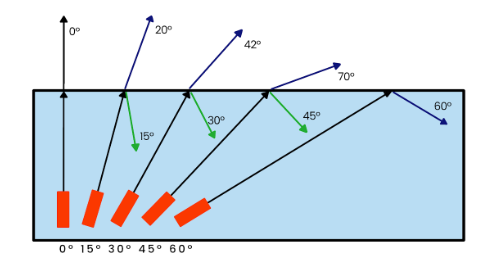
E. Critical Angle
The critical angle represents the angle of incidence at which the refracted ray exits at a 90° angle to the normal, as depicted in Figure 3. When the angle of incidence is equal to the critical angle (Өc), the refracted light exits perpendicular to the normal. The critical angle is the largest angle at which refraction can occur. Any angle of incidence greater than the critical angle will result in total internal reflection.
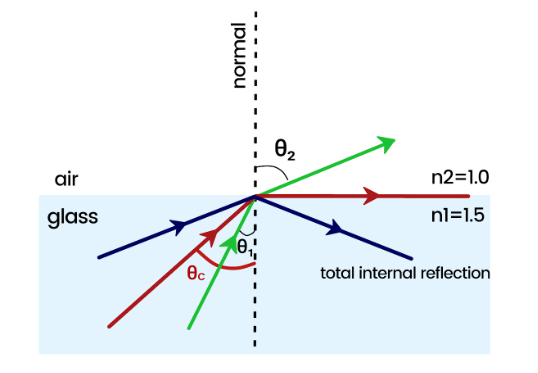
F. Optical Fibres
Optical fibers are communication cables that have revolutionized the transmission of data in medical instruments such as endoscopes, as well as in telephones, the internet, and cable TV. The use of optical fibers has led to high-speed internet access, as demonstrated in Figure 4, which depicts how an optical fiber transports light waves.
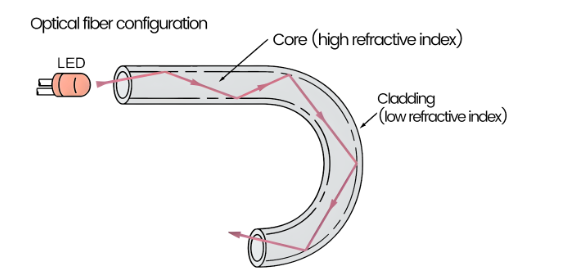
As illustrated in the figure above, an optical fiber consists of a slender glass core surrounded by a cladding of glass with a lower refractive index than the core. Consequently, when light is directed into the core at an angle exceeding the critical angle (Өc), it undergoes total internal reflection at the boundary between the core and the cladding. The light subsequently travels along the fiber via a series of reflections before exiting at the other end.
G. Summary
- The direction of a wave changes when its speed changes, which is known as refraction.
- The angle between the incident ray and the normal is called the angle of incidence (i).
- The angle between the refracted ray and the normal is called the angle of refraction (r).
- Refractive index is defined as the ratio of the sine of the angle of incidence (sin i) to the sine of the angle of refraction (sin r).
- Total internal reflection occurs when a ray of light reflects inside a medium instead of refracting, resulting in no refraction and following the law of reflection.
- The critical angle is the angle of incidence that results in the refracted ray leaving at an angle of 90° to the normal.
- In fiber optic cables, light enters the fiber at the critical angle and travels through the cable via a series of reflections before exiting at the other end.
Refraction is the bending of light as it passes from one medium to another, caused by a change in the speed of light. This change in speed occurs because the density of the medium changes, which alters the refractive index of the medium.
Snell’s law describes the relationship between the angles of incidence and refraction when light passes through a boundary between two different media. It states that the ratio of the sines of the angles of incidence and refraction is equal to the ratio of the refractive indices of the two media.
The critical angle is the angle of incidence that produces an angle of refraction of 90 degrees when light passes from a more dense medium to a less dense medium. When the angle of incidence exceeds the critical angle, total internal reflection occurs.
Total internal reflection is the complete reflection of light at the boundary between two media, caused by the angle of incidence being greater than the critical angle. This phenomenon is used in many optical devices, such as prisms, optical fibers, and binoculars.
The refractive index of a medium determines how much the light will bend as it passes through that medium. The higher the refractive index, the more the light will bend, and the slower it will travel through the medium.
Refraction is the bending of light as it passes through a medium, while reflection is the bouncing back of light when it hits a surface. Refraction occurs when light passes from one medium to another, while reflection occurs when light hits a surface.
Refraction and internal reflection have many practical applications, including the design of lenses for cameras, telescopes, and eyeglasses, the use of fiber optics in communication systems, and the creation of optical illusions in art and entertainment.
The refractive index of a material can be measured using a refractometer, which measures the angle of refraction of a beam of light as it passes through the material. The refractive index can also be calculated using Snell’s law and the angle of incidence and refraction.





Still got a question? Leave a comment
Leave a comment