Rearranging Equations
It is possible to represent an equation with respect to the alternative variable.
For example, P = 16 – 2Q
To transform the equation into a different form Q = you need to transfer each term to the opposite side of the equal sign using inverse operations until the only variable left Q is on the left-hand side.
e.g. Rearrange the equation P = 16 – 2Q to isolate and make Q the subject of the equation
P = 16 – 2Q
P + 2Q = 16 To transfer the variable -2Q to the opposite side of the equation, you can add 2Q to both sides of the equal sign.
2Q = 16 – P You can move the variable P to the other side of the equation by subtracting P from both sides of the equal sign.
If we divide both sides by 2
given a value for P we can determine the value of Q
e.g. Find when
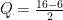
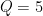
It is possible that you have learned a set of principles for manipulating equations in a previous algebra class. However, it is always beneficial to remind ourselves of these principles. So, let’s revisit them:
- PRINCIPLE #1: You can add, subtract, multiply, or divide by any value, as long as you perform the same operation on both sides of the equation. In an equation, the equal sign functions like a balancing point: if you add a certain value to one side of the balance, you must add the same amount to the other side to maintain balance. The same is true for equations – performing the same operation on both sides preserves the equation’s meaning.
- PRINCIPLE #2: To transfer or eliminate a variable or quantity from one side of the equation, apply the “opposite” operation to it on both sides of the equation. For instance, if you have g-1=w and wish to isolate g, add 1 to both sides of the equation (g-1+1 = w+1). Simplify the equation (because (-1+1)=0) and obtain g = w+1.
Why is it important to rearrange equations?
Surprisingly, there are numerous compelling reasons to improve your equation manipulation skills that are relevant to your field. It can save time, assist with unit conversions, and free up mental capacity. Below are some of the reasons why developing your equation manipulation skills is beneficial (in no particular order):
- It is easier to work with equations prior to substituting numerical values. Moreover, if you can isolate a variable on one side of the equation, it can be utilized to solve any similar problem that requires you to find that variable.
- If you are familiar with equation manipulation, you only need to recall one equation that contains all the variables in question, which can be manipulated to solve for any other variable. This implies less memorization!
- Equation manipulation can aid in keeping track of (or determining) the units of a number. Because units are defined by equations, if you manipulate, substitute values, and eliminate units, you will end up with the exact units (for a given variable).
To rearrange equations in algebra
- Start by applying the same operation to both sides of the equal sign.
- Then, use the inverse operation to move or cancel constants or variables on one side of the equation.
Remember to follow the order of operations! Determine which operation you can perform first.
When you are introduced to an algebraic equation,
It is typically presented with an unfamiliar symbol on the left side of the equal sign and known symbols on the right side. To determine the value of the unknown symbol, you can use mathematical operations on the known quantities.
Indispensable Mathematical Concepts
In order to study AS Level Physics, it is necessary to have a solid understanding of several mathematical techniques.
Quantities and units
Physical quantities are typically represented by symbols or words, such as the symbol “R” for resistance. Each quantity has both a numerical value and a unit of measurement, like 10.5 Ω. When recording data in a table or plotting a graph, only the numerical values are used.
Therefore, headings in tables and labels on graph axes are always written as (physical quantity)/(unit), with the slash representing division. Dividing a physical quantity by its unit results in the numerical value of the quantity.
Resistance is an example of a derived quantity, and the ohm is a derived unit, meaning they are defined in terms of other quantities and units. All derived quantities and units can be expressed in terms of the seven base quantities and units that make up the SI (International System of Units).
A table of the quantities, their units, and symbols is provided. It’s important to note that the candela is not used in AS or A Level Physics.
| Quantity | Unit | Symbol |
| length | metre | m |
| mass | kilogram | kg |
| time | second | s |
| electric current | ampere | A |
| temperature difference | kelvin | K |
| amount of substance | mole | mol |
| luminous intensity | candela | cd |
Equations
In Physics, equations are used to express the relationships between physical quantities. Since different quantities cannot be equal to each other, equations must be homogeneous, meaning the units on both sides of the equation must be identical:
- This has various benefits, such as determining the units of a constant like resistivity and verifying the correctness of an equation.
- If the units on both sides of the equation are the same, the equation may be correct, but if they are different, it is certainly incorrect.
It’s essential to differentiate between a physical quantity and its unit. The value of a physical quantity comprises both the numerical value and the unit of measurement.
When calculating the units of an equation, it’s crucial to distinguish that you’re dealing only with units. You can accomplish this by expressing the units as (quantity) = (unit).
In many cases, equations must be rearranged from the form in which they were originally given or memorized. When rearranging equations, it’s critical to bear in mind that:
- The same mathematical operation must be applied to both sides of the equation.
- Addition or subtraction should be done first, followed by multiplication or division, and finally roots and powers.
As an illustration, suppose we wish to rearrange the equation v2 = u2 + 2as so that we can solve for u:
1. We subtract 2as from both sides of the equation to obtain v2 – 2as = u2.
2 . Then we take the square root of both sides of the equation to get U(v2 – 2as) = u.
For an equation that relates a quantity to the product or quotient of two others, we can use the “magic triangle.” This triangle is divided into three parts, and we start by writing the two quantities that are multiplied or divided in the relationship at the bottom of the triangle.
If one quantity is divided by the other, we write them into the triangle as they would be in a division, with one quantity “over the other.” We then write the remaining quantity into the vacant slot.
An example of this is shown below using V = IR as an illustration, where we write I and R into the triangle first.
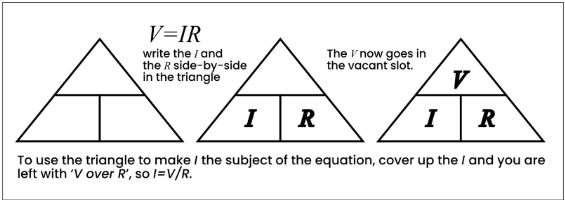
To make I the subject of the equation using the triangle, simply cover up the I and the remaining expression would be ‘V over R’. Therefore, I can be calculated as I = V/R.
Drawing graphs
Physics utilizes graphs in various ways:
- providing an immediate visual representation of the relationship between physical quantities
- determining the values of these quantities
- confirming or disproving hypotheses about the relationship between variables.
However, it is essential to keep in mind that experimental values obtained are not precise, but rather, they are subject to the accuracy and precision of the measuring instrument used and the operator’s skill, as well as any potential changes that may be caused by the instrument itself.
- For instance, when measuring the temperature of a liquid using a thermometer, the manufacturer typically specifies the accuracy (i.e., how reliable the thermometer is), which is typically around ±1°C on a standard laboratory thermometer.
- Additionally, the user’s precision is determined by how closely they read the thermometer (i.e., to the nearest half degree or degree).
- Finally, inserting the thermometer into the substance may alter the temperature of the substance as the two reach thermal equilibrium.
After plotting experimental values on a grid, the graph line is drawn as the most accurate straight line or curve that represents the points, considering the accuracy and precision of the measurements. However, it is important to examine any “anomalous” results, which are points that do not fit the expected straight line or curve. When in doubt about these results, it may be best to disregard them. Nonetheless, it is crucial to make a note in your experimental work explaining why they were disregarded and suggesting possible reasons for the anomalous results.
Measurements and graphs
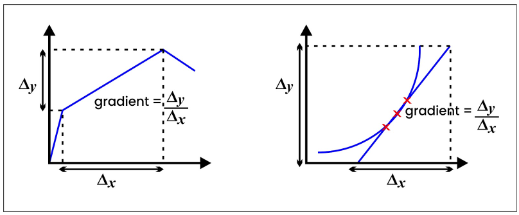
In Physics, certain quantities like velocity, acceleration, and power are defined as the rate of change of one quantity with respect to time. The gradient of a suitable graph can be used to calculate this rate of change. For instance, velocity is determined by the rate of change of displacement with respect to time, and its value can be calculated from the gradient of a displacement-time graph. To calculate the gradient of a straight line or a smooth curve, different methods are used. When working with a straight line:
- First, determine the change in the value of the quantity plotted on the y-axis (Δy) using the entire straight line segment of the graph.
- Next, determine the corresponding change in the value of the quantity plotted on the x-axis (Δx).
- Finally, calculate the gradient by dividing Δy by Δx.
When working with a smooth curve, the gradient is determined by drawing a tangent to the curve and using the same method as described above to calculate the gradient of the tangent.
To draw a tangent to a curve, follow these steps:
- Mark the point on the curve where the gradient needs to be determined.
- Use a compass to mark two points on the curve, which are close to the point where the gradient is to be calculated and equidistant from it.
- Use a ruler to connect these two points, and extend the line beyond each point.
The diagrams below illustrate these techniques.
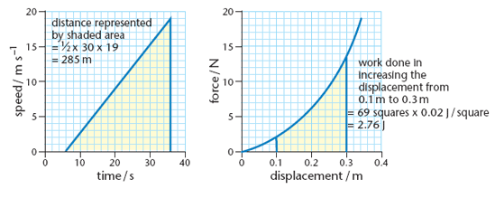
The space between a graph line and the horizontal axis, commonly referred to as the “area under the graph,” can provide valuable insights. This is especially true when the product of the quantities plotted on the axes represents another physical quantity. For instance, on a speed-time graph, this area represents the distance traveled.
If the graph line is a straight line, the area can be calculated as that of the corresponding geometric shape. However, when the graph line is curved, the method of “counting squares” is employed to determine the area.
- Count the number of complete squares between the graph line and the horizontal axis.
- If a fraction of a square is under the line and it is at least half of the square, count it as ‘1’, otherwise count it as ‘0’.
- To determine the physical significance of each square, multiply the quantities represented by one grid division on each axis.
Equations from graphs
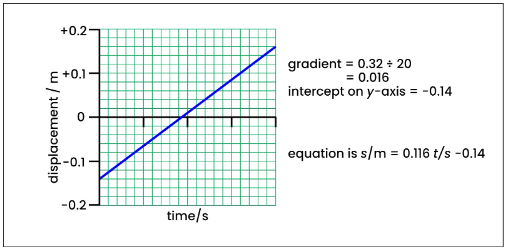
Plotting the values of two variable quantities on a graph can help determine the relationship between them. When the graph is a straight line, it follows an equation in the form of y = mx + c.
Here, m is the gradient of the graph and c is the value of y when x is zero, or the intercept on the y-axis. The relationship between the variables is determined by finding the values of m and c.
The graph below depicts how the displacement, s, of an object varies with time, t.
Trigonometry and Pythagoras
The concepts of Trigonometry and Pythagoras involve the relationships between the angles and sides of a right-angled triangle, which is labeled with the letters o (opposite), a (adjacent), and h (hypotenuse) as shown below:
- sin θ = o/h
- cos θ = a/h
- tan θ = o/a
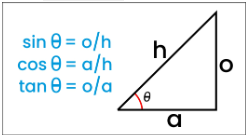
Pythagoras’ theorem states that the square of the length of the hypotenuse (h) is equal to the sum of the squares of the lengths of the other two sides (a and o): h2 = a2 + o2.
Multiples and submultiples
In order to meet the expectations in AS Physics, it is necessary to have a good understanding of the multiples of units listed below:
| Name | Multiple | Symbol |
| micro- | 10-6 | µ |
| milli- | 10-3 | m |
| kilo- | 103 | k |
| mega- | 106 | M |
| giga- | 109 | G |
An illustration of the use of symbols to represent values is seen in the case of MHz which stands for 1×106 Hz, and mN that represents 1×10-3 N.
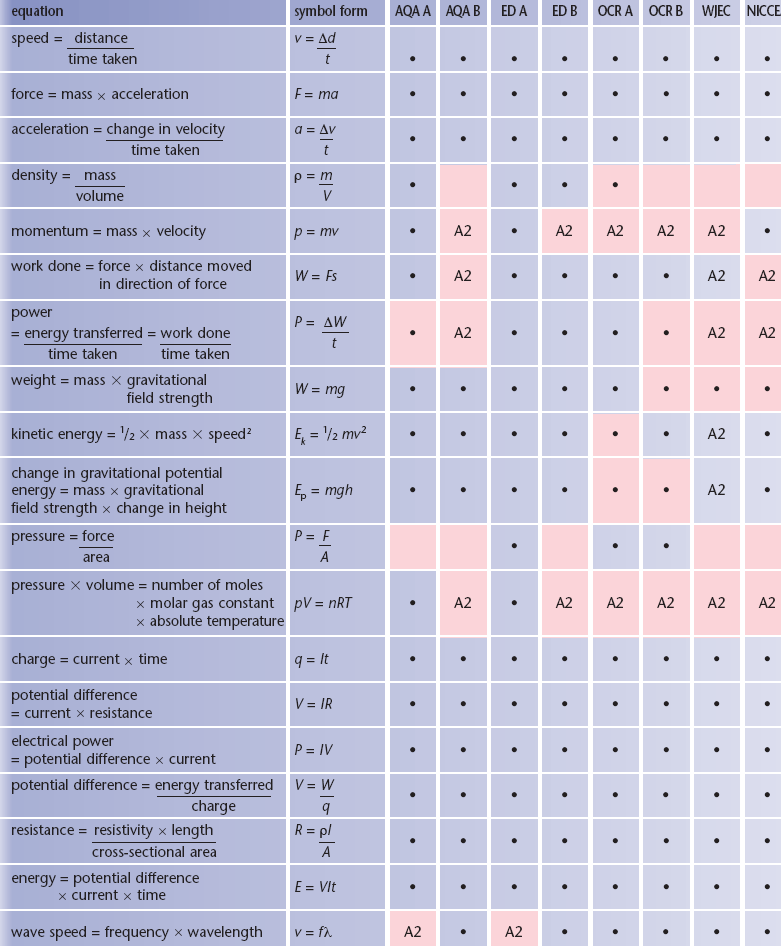
The following is a compilation of equations that may be required,
but are not supplied in topic tests or end-of-course exams. It is important to note that not all of these equations are necessary for every specification, as some are exclusively for A Level and not for AS specification. The table displays the equations that are necessary for each AS specification. All other equations that are needed will be given on a data sheet, which includes the values of physical constants as well.
Rearranging equations is the process of changing the order of terms in an equation so that it is written in a different form but is still mathematically equivalent.
Rearranging equations is an important skill in many areas of mathematics and science. It allows you to manipulate equations in order to solve problems and better understand the relationships between different variables.
There are several methods for rearranging equations, including adding or subtracting terms from both sides of the equation, multiplying or dividing both sides of the equation by a constant, and isolating a variable by moving all other terms to the other side of the equation.
When you rearrange an equation, you must ensure that both sides of the equation remain equal. You can check your work by plugging in values for the variables and confirming that the original equation and the rearranged equation produce the same result.
Some tips for successfully rearranging equations include working step-by-step, writing down each step as you go, keeping track of signs and operations, and practicing frequently to build your skills.
Some common mistakes to avoid when rearranging equations include forgetting to distribute signs properly, canceling terms incorrectly, and making arithmetic errors. It’s important to take your time and double-check your work to avoid these mistakes.
There are many resources available for practicing rearranging equations, including textbooks, online tutorials, and practice problems. You can also create your own practice problems by taking equations from textbooks or other sources and rearranging them in different ways.





Still got a question? Leave a comment
Leave a comment