Centripetal Acceleration
What is Centripetal Acceleration?
Centripetal acceleration refers to the acceleration experienced by a body traversing a circular path. Since velocity is a vector quantity (that is, it has both a magnitude, the speed, and a direction), a body moving in a circular path undergoes constant changes in direction, causing a change in velocity and resulting in acceleration. This acceleration always points towards the center of the circle and is known as centripetal acceleration. The magnitude of centripetal acceleration (ac) is given by v²/r, where v is the speed of the body along the curve and r is the distance from the center of the circle to the moving body. The unit of centripetal acceleration is meter per second squared. The force responsible for this acceleration is directed towards the center of the circle and is known as centripetal force.
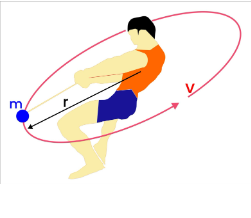
Centripetal Acceleration
Centripetal acceleration refers to the characteristic of an object moving in a circular path and experiencing an acceleration vector directed towards the center of the circle. This type of acceleration is called centripetal acceleration, and it can be observed in various everyday scenarios. For instance, when driving a car in a circular path, the car experiences centripetal acceleration. Similarly, a satellite orbiting the Earth also follows a centripetal acceleration. The term “centripetal” signifies the direction towards the center.
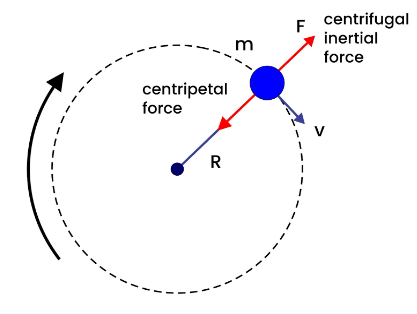
Centripetal Force
The acceleration directed towards the center of a circle has a magnitude that equals the square of the speed of the body along the curve, divided by the total distance from the center of the circle to the moving body. This acceleration is known as centripetal acceleration. The force responsible for causing this acceleration always points towards the center of the circle and is called centripetal force.
Centripetal Acceleration Formula
Acceleration is typically measured in meters per second and represents the rate at which an object’s velocity changes per second. In the case of circular motion, acceleration can be determined by using the following equation:
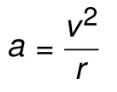
Where,
- The symbol “ac” represents the centripetal acceleration and its unit is meters per second squared (m/s²).
- The symbol “v” represents velocity, and its unit is meters per second (m/s).
- The symbol “r” denotes radius, and its unit is meters (m).
Acceleration refers to the change in velocity of an object. One might wonder how an object moving at a constant speed in a circular path can still have acceleration. While speed simply refers to how fast an object is moving, it is scalar and lacks direction. In contrast, velocity includes both speed and direction and is a vector quantity. For instance, speed can be expressed as “5 miles per hour,” while velocity would be “5 miles per hour south.”
Centripetal acceleration is always caused by a force, such as gravity in the case of a satellite, tension in the string for a swing-ball, or friction between a car and the road when it moves in a circular path. If the centripetal acceleration is removed, the object will continue to move in a straight line tangent to the circle.
Important Questions With Answers
Q1. What is the name of the force that causes an object to deviate from a straight path and move in a circular path?
Ans: The centripetal force is responsible for curving the straight path of an object and making it move in a circular path.
Q2. How are centripetal force and centripetal acceleration similar to each other?
Ans: Centripetal force and centripetal acceleration share a similarity in that they both have a direction pointed towards the center of the circular path.
Q3. What is the metric unit used for measuring centripetal acceleration?
Ans: The metric unit used for measuring centripetal acceleration is meters per second squared (m/s²).
Q4. What is the dimensional formula for centripetal acceleration?
Ans: The dimensional formula for centripetal acceleration can be derived by:
substituting the dimensional formulas of velocity M0L1T-1 and radius M0L1T0 in the centripetal acceleration formula.
Thus, the dimensional formula of centripetal acceleration is M⁰L¹T⁻², where M represents mass, L represents length, and T represents time.
Centripetal Acceleration is the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and its magnitude is given by the formula a = v^2/r, where v is the velocity of the object and r is the radius of the circle.
Centripetal Force is the force that causes an object to move in a circular path. It is given by the formula F = m*a, where m is the mass of the object and a is its Centripetal Acceleration.
Centripetal force is the force that keeps an object moving in a circular path and is always directed towards the center of the circle. Centrifugal force, on the other hand, is the apparent force that seems to push an object away from the center of the circle. However, centrifugal force is not a real force but an apparent force that arises due to the inertia of the object.
Centripetal Acceleration is directly proportional to the square of the Velocity and inversely proportional to the radius of the circle. This relationship is given by the formula a = v^2/r.
Centripetal Force is directly proportional to the Mass of the object and its Centripetal Acceleration. This relationship is given by the formula F = m*a.
Centripetal Acceleration is used in various real-world applications such as amusement park rides, the centrifuge used in medical laboratories, and the motion of planets around the sun.
The period of a circular motion is the time taken by an object to complete one full revolution around the circle. It is given by the formula T = 2πr/v, where r is the radius of the circle and v is the velocity of the object.
Some common mistakes to avoid while solving Centripetal Acceleration problems include using the wrong formula, using the wrong units, and ignoring the direction of the force or acceleration. It’s important to carefully read the problem statement and understand what is being asked before attempting to solve it.





Still got a question? Leave a comment
Leave a comment